
����Ŀ����ͼ�����ڣ���ƽ��ֱ������ϵ�У�һ�߳�Ϊ2�ĵȱ����ǰ�CDEǡ��������ϵ�е���OAB�غϣ��ֽ����ǰ�CDE�Ʊ�AB���е�G��G��Ҳ��DE���е㣩����˳ʱ�뷽����ת180������C��ED��λ�ã�
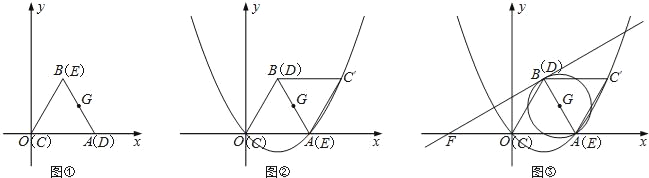
��1����C��������ꣻ
��2����O��A��C������������ߵĽ���ʽ��
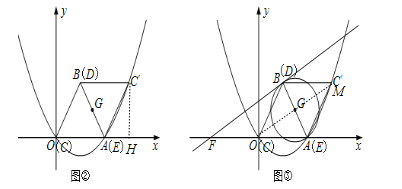
��3����ͼ������G����ABΪֱ����Բ����B������G��������x���ཻ�ڵ�F��������BF�Ľ���ʽ��
��4���ڣ�3���������£����������Ƿ����һ��M��ʹ����BOF����AOM���ƣ������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1) C�䣨3��![]() ��(2) y=
��(2) y=![]() x2��
x2��![]() x (3) y=
x (3) y=![]() x+
x+![]() ��4������
��4������
����������������1����C��H��x������ͼ�������õȱ������κ���ת�����ʵõ�AC��=OA=2����OAB=��BAC��=60�㣬���C��AH=60�㣬Ȼ����ݺ�30�ȵ�ֱ�����������ߵĹ�ϵ�����AH=1��C��H=![]() ���Ӷ��õ�C�����������
���Ӷ��õ�C�����������
��2���������߽���ʽΪy=ax��x��2����Ȼ���C��������������a����
��3���������ߵ����ʵ�AB��BF�������á�FAB=60���õ�FA=2AB=4������F����2��0�������ж��ı���AOBC��Ϊ���������д��B��1��![]() ����Ȼ�����ô���ϵ������ֱ��BF�Ľ���ʽ��
����Ȼ�����ô���ϵ������ֱ��BF�Ľ���ʽ��
��4���������ߵĶԳ���Ϊֱ��x=1�������ߵĶ�������Ϊ��1����![]() �������жϡ�OBFΪ����Ϊ120���ĵ�������������������AM=AO=2ʱ����M���C���غ�����BOF���AOM�������ô�ʱM�����������OM=OAʱ����M���C������ֱ��x=1�Գ�����BOF���AOM�������ô�ʱM����������MA=MOʱ����MΪ�����ߵĶ���ʱ����OAM=120�㣬���жϡ�BOF���AOM�������Ӷ��õ���ʱM������꣮
�������жϡ�OBFΪ����Ϊ120���ĵ�������������������AM=AO=2ʱ����M���C���غ�����BOF���AOM�������ô�ʱM�����������OM=OAʱ����M���C������ֱ��x=1�Գ�����BOF���AOM�������ô�ʱM����������MA=MOʱ����MΪ�����ߵĶ���ʱ����OAM=120�㣬���жϡ�BOF���AOM�������Ӷ��õ���ʱM������꣮
�������1����C��H��x������ͼ����
�ߡ�CDE�͡�OABΪȫ�ȵĵȱ��������������ǰ�CDE�Ʊ�AB���е�G��G��Ҳ��DE���е㣩����˳ʱ�뷽����ת180���õ���C��ED����AC��=OA=2����OAB=��BAC��=60�㣬���C��AH=60�㣬��AH=![]() AC��=1��C��H=
AC��=1��C��H=![]() AH=
AH=![]() ����C�䣨3��
����C�䣨3��![]() ����
����
��2���������߽���ʽΪy=![]() ���������a31=
���������a31=![]() �������a=
�������a=![]() ���������߽���ʽΪy=
���������߽���ʽΪy=![]() x��x��2������y=
x��x��2������y=![]() x2��
x2��![]() x��
x��
��3����BFΪ��G����������AB��BF������FAB=60�㣬��FA=2AB=4����F����2��0����
��OB=OA=AC��=BC��=2�����ı���AOBC��Ϊ��������B��1��![]() ������ֱ��BF�Ľ���ʽΪy=kx+b����F����2��0����B��1��
������ֱ��BF�Ľ���ʽΪy=kx+b����F����2��0����B��1��![]() ���������
���������![]() �������
�������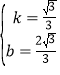 ����ֱ��BF�Ľ���ʽΪy=
����ֱ��BF�Ľ���ʽΪy=![]() x+
x+![]() ��
��
��4�����ڣ�
�����ߵĶԳ���Ϊֱ��x=1����x=1ʱ��y=![]() x2��
x2��![]() x=��
x=��![]() ���������ߵĶ�������Ϊ��1����
���������ߵĶ�������Ϊ��1����![]() ����
����
��OF=OB=2�����OBFΪ����Ϊ120���ĵ�������������AM=AO=2ʱ����M���C���غ�����BOF���AOM��������ʱM��3��![]() ������OM=OAʱ����M���C������ֱ��x=1�Գ�����BOF���AOM��������ʱM����1��
������OM=OAʱ����M���C������ֱ��x=1�Գ�����BOF���AOM��������ʱM����1��![]() ������MA=MOʱ����MΪ�����ߵĶ���ʱ����OAM=120�㣬��BOF���AOM��������ʱM��1����
������MA=MOʱ����MΪ�����ߵĶ���ʱ����OAM=120�㣬��BOF���AOM��������ʱM��1����![]() ����
����
��������������������M���������3��![]() ����1��
����1��![]() ����1����
����1����![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
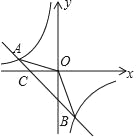
����Ŀ����8�֣���֪A����4��m+10����B��n����4��������һ�κ���y=kx+b�ͷ���������y=![]() ͼ����������㣮
ͼ����������㣮
��1����һ�κ����ͷ����������Ľ���ʽ��
��2�����AOB�������
��3���۲�ͼ��ֱ��д������ʽkx+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ���˶������ü��̶ӵ�������Ҫ15����ɣ����ҹ��̶ӵ�������Ҫ10�����.
��1������üס��ҹ��̶Ӻ���3���ʣ�µĹ������ҹ��̶���ɣ�����Ҫ������?
��2����֪��ÿ��ķ���Ϊ1000Ԫ���Ҷ�ÿ��ķ���Ϊ1600 Ԫ���ӽ�Լ�ʽ�ĽǶȣ���Ϊ�Ǽס��Ҷӵ��������������Ӻ������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������м���ԭ��263ǧ�ˣ�����ԭ��314ǧ�ˣ��ƻ�����������ԭ������A��B���ֲ�Ʒ��100��������һ����Ʒ����Ҫ��ԭ�ϼ������ɱ����±���ʾ��
����ԭ�ϣ���λ��ǧ�ˣ� | ����ԭ�ϣ���λ��ǧ�ˣ� | �����ɱ�����λ��Ԫ�� | |
A��Ʒ | 3 | 2 | 120 |
B��Ʒ | 2.5 | 3.5 | 200 |
��1���ù������е�ԭ���ܷ�֤������Ҫ�����ܣ��м�������������������Ƴ�����
��2��������A��B���ֲ�Ʒ���ܳɱ�ΪyԪ����������A��Ʒx������д��y��x֮��ĺ�����ϵ�������ú���������˵����1�����������������ܳɱ���ͣ���������ܳɱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧΪ�ƽ�����У���裬��ȫУ��Χ��չͼ��Ư���������Ҫ����һ���ס������ֹ���Ư�����ݷ���ͼ�飮��֪һ�����ֹ���Ư�����ݵļ۸��һ�����ֹ���Ư�����ݵļ۸��80Ԫ���������2�����ֹ���Ư�����ݺ�3�����ֹ���Ư�����ݣ�һ����Ҫ����960Ԫ��
��1����ÿ�����ֹ���Ư�����ݺ�ÿ�����ֹ���Ư�����ݵļ۸�ֱ��Ƕ���Ԫ��
��2�����ѧУ�ƻ����������ֹ���Ư�����ݹ�15�������ҹ��������ֹ���Ư�����ݵ��ܷ��ò�����3040Ԫ����ô��ѧУ�����ܹ�����ٸ����ֹ���Ư�����ݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ִ������������Ĺ㷺Ӧ�ã������˿����ҵ�ĸ��ٷ�չ.С���ƻ������ѿ��һ������Ʒ�����˽�ס������ҿ�ݹ�˾�ȽϺ��ʣ���˾��ʾ�������Ʒ������1ǧ�˵ģ���ÿǧ��22Ԫ�շѣ�����1ǧ�ˣ������IJ��ְ�ÿǧ��15Ԫ�շѣ��ҹ�˾��ʾ����ÿǧ��16Ԫ�շѣ����Ӱ�װ��3Ԫ.��С�������Ʒxǧ��.
(1)��x��1ʱ����քeֱ��д���ס������ҿ�ݹ�˾��ݸ���Ʒ�ķ���y(Ԫ)��x(ǧ��)֮��ĺ�����ϵʽ��
(2)��(1)�������£�С��ѡ���ļҿ�ݹ�˾��ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̽����֤����
��������ABCD�У�G������AC��һ���㣨�����A��C�غϣ�����BG����BH��BG����ʹBH��BG����GH��CH��
��1����G��AC�ϣ���ͼ1������ͼ�����ABGȫ�ȵ����������� ����
���߶�AG��CG��GH֮���������ϵ���� ����
��2����G��AC���ӳ����ϣ���ͼ2������ô�߶�AG��CG��BG֮����������������ϵ��д�����۲�����֤����
��Ӧ�ã���3����ͼ3��G��������ABCD�ĶԽ���CA���ӳ����ϣ���BGΪ����������BGMN����AG��2��AD��4����ֱ��д��������BGMN�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
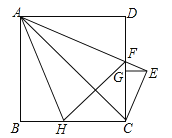
����Ŀ����ͼ���߳�Ϊ2��������ABCD�У�AEƽ�֡�DAC��AE��CD�ڵ�F��CE��AE������Ϊ��E��EG��CD������Ϊ��G����H�ڱ�BC�ϣ�BH=DF������AH��FH��FH��AC���ڵ�M�����½��ۣ�
��FH=2BH����AC��FH����S��ACF=1����CE=![]() AF����
AF����![]() =FGDG��������ȷ���۵ĸ���Ϊ��������
=FGDG��������ȷ���۵ĸ���Ϊ��������
A. 2 B. 3 C. 4 D. 5
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com