
【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)求∠PED的度数.

【答案】(1)见解析;(2)45°
【解析】
(1)根据正方形的性质四条边都相等可得BC=CD,对角线平分一组对角,可得∠ACB=∠ACD,然后利用“边角边”证明△PBC和△PDC全等,根据全等三角形对应边相等可得PB=PD,然后等量代换即可得证;
(2)根据全等三角形对应角相等可得∠PBC=∠PDC,根据等边对等角可得∠PBC=∠PEB,从而得到∠PDC=∠PEB,再根据∠PEB+∠PEC=180°,求出∠PDC+∠PEC=180°,然后根据四边形的内角和定理求出∠DPE=90°,判断出△PDE是等腰直角三角形,根据等腰直角三角形的性质求解即可.
(1)∵四边形ABCD是正方形,
∴BC=CD,∠ACB=∠ACD,
在△PBC和△PDC中,
∵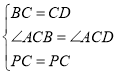 ,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)∵四边形ABCD是正方形,
∴∠BCD=90°,
∵△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
在四边形PECD中,∠EPD=360°(∠PDC+∠PEC)∠BCD=360°180°90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴∠PED=45°.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
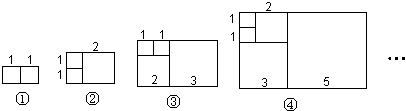
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造正方形,再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形,若按此规律继续作长方形,则序号为⑦的长方形周长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,点M、N位于第一象限,其中M的坐标为(m,5),点N的坐标(n,8),且m≥n.
(1)若MN与坐标轴平行,则MN= ;
(2)若m、n、t满足![]() ,MA⊥x轴,垂足为A,NB⊥x轴,垂足为B.
,MA⊥x轴,垂足为A,NB⊥x轴,垂足为B.
①求四边形MABN的面积;
②连接MN、OM、ON,若△MON的面积大于26而小于30,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林准备进行如下操作实验;把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58cm2,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48cm2.”他的说法对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,
(1)A处是否会受到火车的影响,并写出理由
(2)如果A处受噪音影响,求影响的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形 ABCD中,AB 6cm ,BC 12cm ,B 30,点P 在 BC 上由点B向点C 出发,速度为每秒2cm;点Q 在边AD上,同时由点 D 向点 A 运动,速度为每秒1cm ,当点 P 运动到点C时,P 、Q 同时停止运动,连接 PQ,设运动时间为t秒.
(1)当t为何值时四边形 ABPQ 为平行四边形?
(2)当t为何值时,四边形 ABPQ 的面积是四边形 ABCD 的面积的四分之三?
(3)连接 AP ,是否存在某一时刻t,使ABP 为等腰三角形?并求出此刻t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,在AD上截取AE=AB,连接BE,EO,并求∠BEO的角度(要求:尺规作图,保留痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=6,∠COD=60°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板ABC和三角板BDE(∠ACB=∠DBE=90°,∠ABC=60°)按不同的位置摆放.
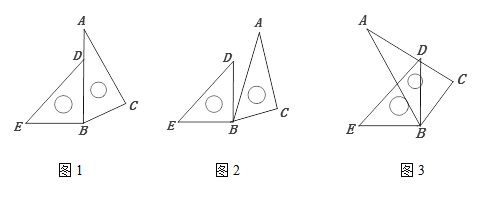
(1)如图1,若边BD,BA在同一直线上,则∠EBC= ;
(2)如图2,若∠EBC=165°,那么∠ABD= ;
(3)如图3,若∠EBC=120°,求∠ABD的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com