
分析 先利用有数的性质判断a<0,b<0,再把原式化简得到原式=-$\sqrt{ab}$•$\frac{a+b}{ab}$,然后利用整体代入的方法计算.
解答 解:∵a+b=-4$\sqrt{2}$<0,ab=8>0,
∴a<0,b<0,
∴原式=$\sqrt{\frac{ab}{{b}^{2}}}$+$\sqrt{\frac{ab}{{a}^{2}}}$
=-$\frac{\sqrt{ab}}{b}$-$\frac{\sqrt{ab}}{a}$
=-$\sqrt{ab}$•$\frac{a+b}{ab}$
=-$\sqrt{8}$×$\frac{-4\sqrt{2}}{8}$
=2.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:解答题
 如图,已知线段AB=10cm,点C为射线AB上的点,且BC=6cm,点M为线段AC的中点、点N为线段BC的中点.
如图,已知线段AB=10cm,点C为射线AB上的点,且BC=6cm,点M为线段AC的中点、点N为线段BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中D、E、F分别是各边的中点,连接AE、DF.
如图,△ABC中D、E、F分别是各边的中点,连接AE、DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
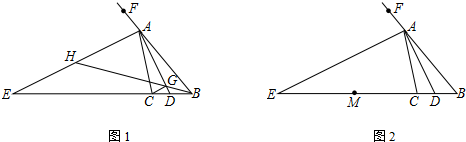
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com