
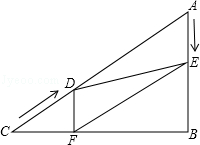
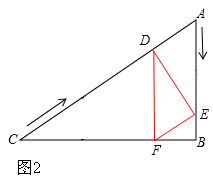
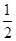 AC=
AC=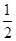 ×60=30cm。
×60=30cm。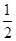 CD=2t。∴DF=AE。
CD=2t。∴DF=AE。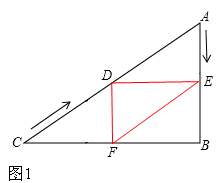
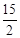 。
。
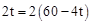 2t =2×60-4t,解得:t=12。
2t =2×60-4t,解得:t=12。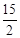 或12时,△DEF为直角三角形
或12时,△DEF为直角三角形

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源:不详 题型:单选题
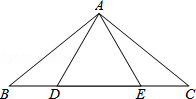
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
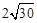 .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=
| A.6 | B.8 | C.10 | D.12 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ;③△PMN为等边三角形;④当∠ABC=45°时,BN=
;③△PMN为等边三角形;④当∠ABC=45°时,BN=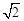 PC.其中正确的个数是
PC.其中正确的个数是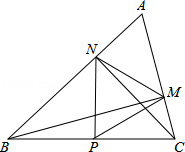
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com