
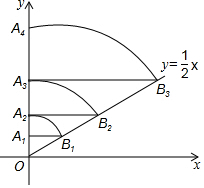
 如图,直线l:y=$\frac{1}{2}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y 轴于点A3,…,按此做法进行下去,OA2017的长为( )
如图,直线l:y=$\frac{1}{2}$x,点A1(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O 为圆心,OB1长为半径画弧交y轴于点A2;再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y 轴于点A3,…,按此做法进行下去,OA2017的长为( )| A. | ($\sqrt{5}$)2016 | B. | ($\sqrt{5}$)2017 | C. | 22016 | D. | 22017 |
分析 首先计算出OA1,A1B1的长,进而得到tan∠B1OA1的值,然后再利用三角函数值计算出OA2、OA3、…进而得到点An(0,2n-1),进而得到答案.
解答 解:由A1坐标为(0,1),可知OA1=1,
把y=1代入直线y=$\frac{1}{2}$x中,得x=2,即A1B1=2,
∴OB1=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴OA2=OB1=$\sqrt{5}$,
同理OA3=($\sqrt{5}$)2,OA4=($\sqrt{5}$)3,
∴OAn=($\sqrt{5}$)n-1.
因此A2017的坐标为($\sqrt{5}$)2016.
故选A.
点评 此题主要考查了一次函数图象上点的坐标特点,关键是掌握凡是函数图象经过的点必能满足解析式.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
 已知一次函数图象经过点(3,5),(-4,-9)两点.
已知一次函数图象经过点(3,5),(-4,-9)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | … | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | 1 | $\frac{3}{2}$ | 3 | 6 | … | -6 | -3 | -$\frac{3}{2}$ | -1 | … |
| A. | 图象在第二、四象限内 | B. | 图象必经过点(6,-$\frac{1}{2}$) | ||
| C. | 图象与坐标轴没有交点 | D. | 当x<-4时,y的取值范围是<$\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-x<b-x | B. | -a+1>-b+1 | C. | 5a>5b | D. | $\frac{a}{3}$<$\frac{b}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
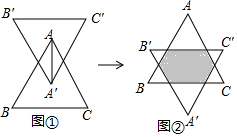 如图①,等边三角形ABC和等边三角形A′B′C′的边长均为2,且BC∥B′C′,将等边三角形ABC沿A′A方向向上平移到图②的位置,则阴影部分的周长为4.
如图①,等边三角形ABC和等边三角形A′B′C′的边长均为2,且BC∥B′C′,将等边三角形ABC沿A′A方向向上平移到图②的位置,则阴影部分的周长为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com