
分析 由方程为一元二次方程即可得出k2-3k+2=(k-1)(k-2)≠0,解之可得出k≠1且k≠2,利用因式分解法解一元二次方程可得出x1=-$\frac{k}{k-1}$、x2=-$\frac{k-1}{k-2}$,由方程的两根均为整数可设$\frac{k}{k-1}$=m,$\frac{k-1}{k-2}$=n(其中m、n均是不为1的整数),分析当k=0时,x1=0、x2=-$\frac{1}{2}$,从而排除m=0的情况,结合k≠1可得出n≠0,解分式方程用含m、n的代数式表示出k值,即k=$\frac{m}{m-1}$=$\frac{2n-1}{n-1}$,用含n的代数式表示出m,结合m、n均为整数即可求出n=-1,将其代入$\frac{k-1}{k-2}$=n即可求出k值,此题得解.
解答 解:∵方程(k2-3k+2)x2+(2k2-4k+1)x+k2-k=0为一元二次方程,
∴k2-3k+2=(k-1)(k-2)≠0,
∴k≠1且k≠2.
∵(k2-3k+2)x2+(2k2-4k+1)x+k2-k=[(k-1)x+k][(k-2)x+k-1]=0,
∴x1=-$\frac{k}{k-1}$,x2=-$\frac{k-1}{k-2}$.
∵一元二次方程(k2-3k+2)x2+(2k2-4k+1)x+k2-k=0有两个不相等的整数根,
∴设$\frac{k}{k-1}$=m,$\frac{k-1}{k-2}$=n(其中m、n均是不为1的整数),
∵当k=0时,x1=0,x2=-$\frac{1}{2}$,
∴m≠0,
∵k±1,
∴n≠0.
∴k=$\frac{m}{m-1}$=$\frac{2n-1}{n-1}$,
∴m=2-$\frac{1}{n}$.
∵m为整数,n为整数,
∴n=-1或n=1(舍去).
∴$\frac{k-1}{k-2}$=-1,
解得:k=$\frac{1}{2}$.
点评 本题考查了一元二次方程的定义、因式分解法解一元二次方程以及解分式方程,解题的关键是利用因式分解法解一元二次方程求出x1=-$\frac{k}{k-1}$,x2=-$\frac{k-1}{k-2}$.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
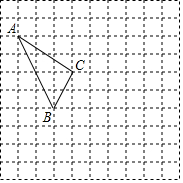 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 +y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )
+y2,阴影部分即为被墨迹弄污的部分.那么被墨汁遮住的一项应是( )| A. | -7xy | B. | -xy | C. | 7xy | D. | xy |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,顶点为M的抛物线y=ax2-x-3与x轴交于点A、B,过点B的直线与抛物线的对称轴相交于点C(2,4),点P是该抛物线在x轴下方部分上的一个动点,过点P的直线y=x+m分别与抛物线的对称轴、直线BC相交于点Q、D.
如图,顶点为M的抛物线y=ax2-x-3与x轴交于点A、B,过点B的直线与抛物线的对称轴相交于点C(2,4),点P是该抛物线在x轴下方部分上的一个动点,过点P的直线y=x+m分别与抛物线的对称轴、直线BC相交于点Q、D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 轴对称是两个图,轴对称图形是一个图 | |
| B. | 若两线段互相垂直平分,则这两线段互为对称轴 | |
| C. | 所有直角三角形都不是轴对称图形 | |
| D. | 两个内角相等的三角形不是轴对称图 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com