
分析 根据题意可知本题需要设两个城市之间的距离为x千米,利用无风时飞机的速度作为相等关系,利用顺风的时间和路程求出的无风时的速度为:$\frac{x}{2\frac{5}{6}}$-24,逆风的时间和路程可求出无风时的速度为:$\frac{x}{3}$+24,列出方程即可求解.
解答 解:设两地距离为x千米,则有方程:
$\frac{x}{2\frac{5}{6}}$-24=$\frac{x}{3}$+24,
解得:x=2448,
$\frac{x}{2\frac{5}{6}}$=$\frac{2448}{2\frac{5}{6}}$=864,
$\frac{x}{3}$=$\frac{2448}{3}$=816.
答:两个城市之间的距离为2448千米,飞机在顺风的速度是864千米/小时,逆风中的速度是816千米/小时.
点评 考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的数量关系,列出方程,再求解.此题的关键是要知道利用无风时飞机的速度作为相等关系.一个量的两种不同表示方法作为相等关系是解一元一次方程应用题中一个重要的相等关系,需要掌握.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
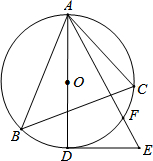 如图,已知△ABC是⊙O的圆内接三角形,AD为⊙O的直径,DE为⊙O的切线,AE交⊙O于点F,∠C=∠E.
如图,已知△ABC是⊙O的圆内接三角形,AD为⊙O的直径,DE为⊙O的切线,AE交⊙O于点F,∠C=∠E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
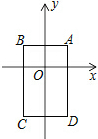 如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是(-1,-2).
如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是(-1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
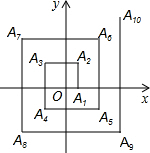 在平面直角坐标系中,点A从原点出发沿x轴正方向移动1个单位到A1,逆时针旋转90°前进2个单位到A2…逆时针旋转90°前进2015个单位到点A2015,则A2015的坐标是(1008,-1006).
在平面直角坐标系中,点A从原点出发沿x轴正方向移动1个单位到A1,逆时针旋转90°前进2个单位到A2…逆时针旋转90°前进2015个单位到点A2015,则A2015的坐标是(1008,-1006).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
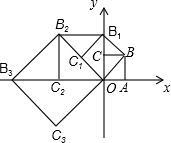 如图,在平面直角坐标系中,有一边长为1的正方形AOBC,边OA,OC分别在x轴,y轴上,以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2…照此规律下去,则点B2015的坐标为(21008,0).
如图,在平面直角坐标系中,有一边长为1的正方形AOBC,边OA,OC分别在x轴,y轴上,以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2…照此规律下去,则点B2015的坐标为(21008,0).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 每天使用零花钱(单位:元) | 0 | 1 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 5 | 4 | 2 |
| A. | 众数是3元 | B. | 平均数是2.5元 | C. | 极差是5元 | D. | 中位数是3元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
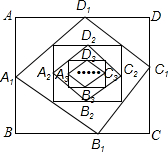 如图所示,已知矩形ABCD,AB=6,BC=8,依次连接矩形ABCD的各边中点构成第一个四边形A1B1C1D1,再依次连接四边形A1B1C1D1的各边中点又得到一个新的四边形A2B2C2D2…,依此类推,当n=2015时,四边形AnBnCnDn的周长为5×($\frac{1}{2}$)2010.
如图所示,已知矩形ABCD,AB=6,BC=8,依次连接矩形ABCD的各边中点构成第一个四边形A1B1C1D1,再依次连接四边形A1B1C1D1的各边中点又得到一个新的四边形A2B2C2D2…,依此类推,当n=2015时,四边形AnBnCnDn的周长为5×($\frac{1}{2}$)2010.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com