
分析 把已知条件写成三个完全平方式的和的形式,再由非负数的性质求得三边,根据勾股定理的逆定理即可判断△ABC的形状.
解答 解:△ABC是直角三角形.
理由:∵a2+b2+c2=10a+24b+26c-338,
∴(a2-10a+25)+(b2-24b+144)+(c2-26c+169)=0
即(a-5)2+(b-12)2+(c-13)2=0
∵(a-5)2≥0,(b-12)2≥0,(c-13)2≥0.
∴a-5=0,得a=5;b-12=0,得b=12;c-13=0,得c=13.
又∵132=52+122,即a2+b2=c2
∴△ABC是直角三角形.
点评 此题考查因式分解的实际运用,非负数的性质,利用完全平方公式分组分解因式是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
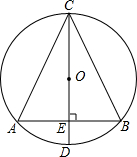 如图,⊙O中,直径CD垂直于弦AB于E,AB=2,连接AC,BC,则tan∠ACB的值的倒数等于线段( )
如图,⊙O中,直径CD垂直于弦AB于E,AB=2,连接AC,BC,则tan∠ACB的值的倒数等于线段( )| A. | AC的长 | B. | AE的长 | C. | OE的长 | D. | CE的长 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com