
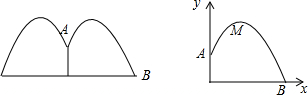
分析 (1)根据题意可设解析式为顶点式形式,由A(0,1)、M(1,2)两点坐标求解析式;
(2)求水池半径即时求当y=0时x的值.
解答 解:(1)设这条抛物线解析式为y=a(x-h)2+k
由题意知:顶点M为(1,2),A为(0,1)
∴k=2,1=a(0-1)2+2,
解得:a=-1.
所以这条抛物线的解析式为y=-(x-1)2+2.
(2)令y=0,则0=-(x-1)2+2,
解得x1≈2.41,x2≈-0.41(舍).
答:若不计其它因素,水池的半径至少2.41米,才能使喷出的水流不至于落在池外.
点评 本题考查二次函数的实际应用,根据实际问题求二次函数,再运用二次函数求最大值.此题为数学建模题,借助二次函数解决实际问题.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:填空题
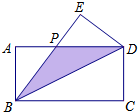 如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.
如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
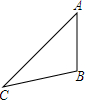 如图,△ABC中,∠B=100°,按要求完成画图并解答问题:
如图,△ABC中,∠B=100°,按要求完成画图并解答问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{a}^{2}-2}$ | B. | $\sqrt{{x}^{2}+2}$ | C. | $\sqrt{3-π}$ | D. | $\root{3}{a}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com