
【题目】在△ABC中∠B=45°,∠C=30°,点D为BC边上任意一点,连接AD,将线段AD绕A顺时针旋转90°,得到线段AE,连接DE.

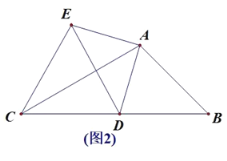
(1)如图1,点E落在BA的延长线上时,∠EDC= (度)直接填空.
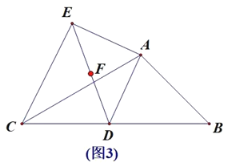
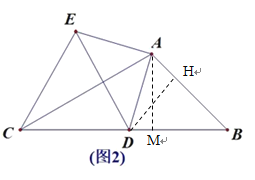
(2)如图2,点D在运动过程中,DE⊥AC时,AB=4 ,求DE的值.
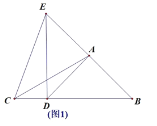
(3)如图3,点F为线段DE中点,AB=![]() ,求出动点D从B运动到C,点F经过的路径长度.
,求出动点D从B运动到C,点F经过的路径长度.
【答案】(1)90°;(2)DE=![]() ;(3)
;(3)![]()
【解析】
(1)利用三角形的外角的性质即可解决问题;
(2)过点A作AM⊥BC于M,过点D作DH⊥AB于H,构建直角三角形,利用特殊角的三角函数值求出BM、CM,设设BH=DH=x,利用三角函数列出方程,求出BD,进而求得答案;
(3)根据主从联动的原理,可知点F的轨迹是线段BC顺时针旋转45度,再缩短为根号二分之一,求出BC即可.
解:(1)如图1,
∵将线段AD绕A顺时针旋转90°,得到线段AE,
∴AE=AD,∠AED=∠ADE=45°
∵∠B=45°,
∴∠EDC=∠B+∠AED=90°
故答案为:90°
(2)如图2,过点A作AM⊥BC于M,过点D作DH⊥AB于H,
在Rt△ABM中,∠B=45°, AM⊥BC,AB=4,
∴AM=BM=![]()
在Rt△DHB中,∠B=45°, DH⊥AB,设BH=DH=x,
∴BD=![]()
在Rt△AMC中,∠AMC=90°, ∠ACB=30°,
∴![]()
∴![]()
∴CM=![]()
∵DE⊥AC,AE=AD
∴AC是线段DE的垂直平分线,
∴CD=CE,∠ECA=∠DCA=30°
∴∠ECD=60°
∴△CDE是等边三角形
∴∠EDC=60°,CD=DE
∴∠ADH=180°-∠EDC-∠ADE-∠BDH=30°
在Rt△ADH中,AH=4-x,
∴tan∠ADH=![]()
∴AH=![]()
∴![]() =4-x,
=4-x,
∴![]()
∴BD=![]()
∴DM=BD-BM=![]() =
=![]()
∴CD=CM-DM=![]() -(
-(![]() )=
)=![]()
∴DE=![]()
(3)如图3,连接AF,过A作AM⊥BC,
∵△ADE为等腰直角三角形,F为ED中点,
∴∠DAF=45°,![]()
∴AF相当于AD逆时针旋转了45°,再变为![]() AD,
AD,
又∵点D轨迹为BC,∴点F的轨迹为BC逆时针旋转45°,再变为![]() BC,
BC,
在等腰Rt△ABM中,AB=![]() ,∴AM=BM=
,∴AM=BM=![]()
在Rt△ACM中,∠ACM=30°,
∴tan30°=![]() ,
,
∴CM=![]()
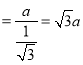
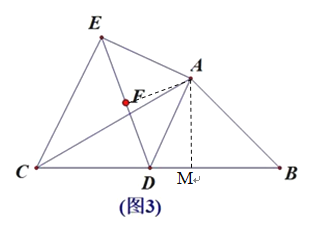
∴BC=CM+BM=![]()
∴点F的路径为:![]() BC=
BC=![]()
所以点F的路径为:![]()


科目:初中数学 来源: 题型:
【题目】喜迎新中国70华诞,感受祖国70年沧桑巨变,70年壮丽辉煌,西大附中开展“祖国,我为你骄傲”的歌唱比赛,为了筹集歌唱比赛的演出服装资金,初二年级从批发市场购进![]() 、
、![]() 两种材料用于手工制作,进行“爱心义卖”.若每个
两种材料用于手工制作,进行“爱心义卖”.若每个![]() 种材料的进价比每个
种材料的进价比每个![]() 种材料的进价少2元,且用160元购进
种材料的进价少2元,且用160元购进![]() 种材料的数量与用200元购进
种材料的数量与用200元购进![]() 种材料的数量相等.
种材料的数量相等.
(1)求![]() 、
、![]() 两种材料的进价分别为多少元?
两种材料的进价分别为多少元?
(2)同学们齐心协力、大胆创新制作出了新颖别致的甲、乙两种手工艺品共56个,乙的数量比甲的数量的两倍还多,但多的个数不超过2个,甲的售价是24元/个,乙的售价是30元/个,为了使利润不低于1040元,有几种制作方案,哪种利润方案最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随机抽取某城市天的空气质量状况统计如下:
污染指数( |
|
|
|
|
|
|
天数( |
|
|
|
|
|
|
(其中![]() 时,空气质量为优;
时,空气质量为优;![]() 时,空气质量为良;
时,空气质量为良;![]() 时,空气质量为轻微污染)
时,空气质量为轻微污染)
(1)这![]() 天中,空气质量为轻微污染的天数所占的百分数是多少?
天中,空气质量为轻微污染的天数所占的百分数是多少?
(2)估计该城市一年(以![]() 天记)中有多少天空气质量到良以上?
天记)中有多少天空气质量到良以上?
(3)保护环境人人有责,请说出一种保护环境的好方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.
(x>0)的图象交于A(m,4),B(2,n)两点,与坐标轴分别交于M、N两点.
(1)求一次函数的解析式;
(2)根据图象直接写出不等式kx+b﹣![]() >0的解集;
>0的解集;
(3)求△AOB的面积;
(4)若点P在x轴上、点Q在y轴上,且以P、Q、A、B为顶点的四边形是平行四边形,请直接写出点P、Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列给出的条件中,能判定四边形ABCD为平行四边形的是()
A.AB=BC,CD=DAB.AB//CD,AD=BC
C.AB//CD,∠A=∠CD.∠A=∠B,∠C=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________
的正方形AEFG按图(1)位置放置,AD与AE在同一直线上,AB与AG在同一直线上,将正方形ABCD绕点A逆时针旋转如图(2),线段DG与线段BE相交,交点为H,则△GHE与△BHD面积之和的最大值为_________ 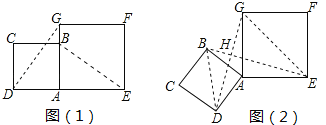
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com