练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

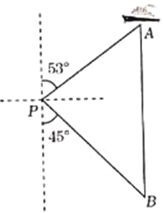
    【题目】如图， 一艘海轮位于灯塔的北偏东方向．距离灯塔海里的处，它沿正南方向航行一段时间后．到达位于灯塔的南偏东方向上的处．

    （1）求出处与灯塔的距离(结果取整数)；

    （2）用方向和距离描述灯塔相对于处的位置．(参考数据：，，)

    【答案】（1）处与灯塔的距离约为海里；（2）灯塔位于处北偏西方向，且距离处约海里．

    【解析】

    （1）根据方向角的定义结合已知条件在图中画出点B，作PC⊥AB于C，先解Rt△PAC，得出PC=PAsin∠PAC=80，再解Rt△PBC，得出PB=PC=1.41×80≈113；
    （2）由∠CBP=45°，PB≈113海里，即可得到灯塔P位于B处北偏西45°方向，且距离B处约113海里．

    解：如图，

    作于点

    在中

    在中，

    即

    答：处与灯塔的距离约为海里．

    海里

    灯塔位于处北偏西方向，

    且距离处约海里

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（2017·泰安）如图，是将抛物线平移后得到的抛物线，其对称轴为，与轴的一个交点为，另一交点为，与轴交点为．

    （1）求抛物线的函数表达式；

    （2）若点为抛物线上一点，且，求点的坐标；

    （3）点是抛物线上一点，点是一次函数的图象上一点，若四边形为平行四边形，这样的点是否存在？若存在，分别求出点的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

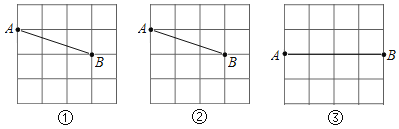
    【题目】图①，图②，图③均为4×4的正方形网格，每个小正方形的顶点称为格点，小正方形的边长都为1．线段AB的端点均在格点上． 按要求在图①，图②，图③中画图．

    （1）在图①中，以线段AB为斜边画一个等腰直角三角形，且直角的顶点为格点；

    （2）在图②中，以线段AB为斜边画一个直角三角形，使其面积为2，且直角的顶点为格点；

    （3）在图③中，画一个四边形，使所画四边形是中心对称图形，不是轴对称图形，且其余两个顶点均为格点.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

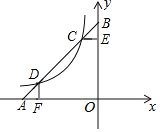
    【题目】如图，直线y1＝x+b与x轴、y轴分别交于A，B两点，与反比例函数y2＝﹣（x＜0）的图象交于C，D两点，点C的横坐标为﹣1，过点C作CE⊥y轴于点E，过点D作DF⊥x轴于点F．下列说法正确的是（　　）

    A.b＝5

    B.BC＝AD

    C.五边形CDFOE的面积为35

    D.当x＜﹣2时，y1＞y2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

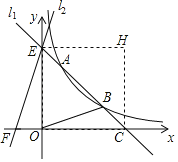
    【题目】如图，直线l1：y＝kx+b与双曲线y＝（x＞0）交于A，B两点，与x轴交于点C，与y轴交于点E，已知点A（1，3），点C（4，0）．

    （1）求直线l1和双曲线的解析式；

    （2）将△OCE沿直线l1翻折，点O落在第一象限内的点H处，求点H的坐标；

    （3）如图，过点E作直线l2：y＝3x+4交x轴的负半轴于点F，在直线l2上是否存在点P，使得S△PBC＝S△OBC？若存在，请直接写出所有符合条件的点P的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠A=90°，AB=AC，BC=20，DE是△ABC的中位线，点M是边BC上一点，BM=3，点N是线段MC上的一个动点，连接DN，ME，DN与ME相交于点O．若△OMN是直角三角形，则DO的长是______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，二次函数图象的对称轴为直线，且，顶点为．

    （1）求的值；

    （2）求点的坐标（用含的式子表示）；

    （3）已知点，，若函数的图象与线段恰有一个公共点，直接写出的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着某市养老机构（养老机构指社会福利院、养老院、社区养老中心等）建设稳步推进，拥有的养老床位及养老建筑不断增加．

    （1）该市的养老床位数从2017年底的2万个增长到2019年底的2.88万个，求该市这两年（从2017年底到2019年底）拥有的养老床位数的平均年增长率；

    （2）该市某社区今年准备新建一养老中心，如果计划赡养200名老人，建筑投入平均5万元/人，且计划赡养的老人每增加5人，建筑投入平均减少1000元/人，那么新建该养老中心需申报的最高建筑投入是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与轴交于点，与轴交于点，将线段绕点顺时针旋转90°得到线段，反比例函数的图象经过点．

    （1）求直线和反比例函数的解析式；

    （2）已知点是反比例函数图象上的一个动点，求点到直线距离最短时的坐标．

    查看答案和解析>>

    同步练习册答案