
 19、如图,设P(x,0)是x轴上的一个动点,它与x轴上表示-2的点的距离为y,求x的函数y的解析式.画出这个函数的图象;根据图象直接写出x为何值时,函数大于是2.
19、如图,设P(x,0)是x轴上的一个动点,它与x轴上表示-2的点的距离为y,求x的函数y的解析式.画出这个函数的图象;根据图象直接写出x为何值时,函数大于是2.科目:初中数学 来源: 题型:
| MT | RT |

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
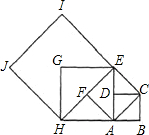 阅读下面的文字,回答后面的问题.
阅读下面的文字,回答后面的问题.| 3101-3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
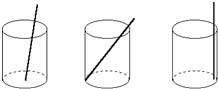 11、将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,如图,设筷子露出在杯子外面长为hcm,则h的取值范围是
11、将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,如图,设筷子露出在杯子外面长为hcm,则h的取值范围是查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com