
����Ŀ����ͼ1����O���߶�AB�ϣ�AO��4��OB��2��OCΪ���ߣ��ҡ�BOC��60��������P��ÿ��2����λ���ȵ��ٶȴӵ�O������������OC���˶������˶�ʱ��Ϊt�룮
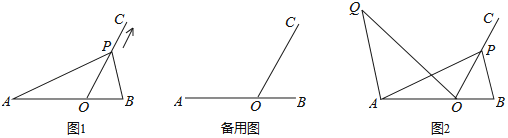
��1����t��1��ʱ����OP���� ����S��ABP���� ����
��2������ABP��ֱ��������ʱ����t��ֵ��
��3����ͼ2����AP��ABʱ������A��AQ��BP����ʹ�á�QOP����B����AQBP��ֵ��Ϊ����AQBP��ֵ��С��ͬѧ���Թ�O����OE��AP��BP�ڵ�E��������С��ͬѧ�����ǵ�������ȫͼ�β���AQBP��ֵ��
���𰸡���1��2��3![]() ����2������ABP��ֱ��������ʱ��t��2��t��
����2������ABP��ֱ��������ʱ��t��2��t��![]() ����3����ȫͼ�μ�������AQPB��12��
����3����ȫͼ�μ�������AQPB��12��
��������
��1����PD��AB�ڵ�D���������Ǻ�����⣻
��2������ABP��ֱ��������ʱ���֡�A��90������B��90������APB��90����������Ӧͼ�Σ�����30������Ե�ֱ�DZߵ���б�ߵ�һ�뼰���ɶ�����⣻
��3������O��OE��AP����PB�ڵ�E������һ�����������Σ�����OAQ�ס�PEO�����ö�Ӧ�߳ɱ������.
��1����t��1��ʱ��OP��2t��2��1��2��
���ͼ1������P��PD��AB�ڵ�D��
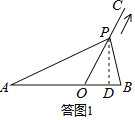
��Rt��POD��PD��OPsin60����2��![]() ��
��![]() ��
��
��S��ABP��![]() ABPD��
ABPD��![]() ����4+2����
����4+2����![]() ��3
��3![]() ��
��
�ʴ�Ϊ��2��3![]() ��
��
��2������ABP��ֱ��������ʱ��
������A��90����
�ߡ�BOC��60���ҡ�BOC����A��
���A��90�����ʴ������β����ڣ�
������B��90�������ͼ2��ʾ��
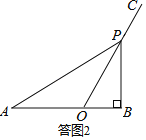
�ߡ�BOC��60����
���BPO��30����
��OP��2OB��4����OP��2t��
��t��2��
������APB��90�������ͼ3��ʾ��
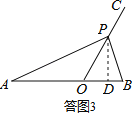
����P��PD��AB�ڵ�D����OD��OPsin30����t��PD��OPsin60����![]() t��
t��
��AD��OA+OD��4+t��BD��OB-OD��2-t��
��Rt��ABP�У��ɹ��ɶ����ã�PA2+PB2��AB2
�ࣨAD2+PD2��+��BD2+PD2����AB2��
��[��4+t��2+��![]() t��
t��![]() t��2]��62��
t��2]��62��
�ⷽ�̵ã�t��![]() ��t��
��t��![]() ����ֵ��ȥ����
����ֵ��ȥ����
��t��![]() ��
��
��������������ABP��ֱ��������ʱ��t��2��t��![]() ��
��
��3�����ͼ4������O��OE��AP����PB�ڵ�E��
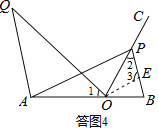
����![]() ��
��![]() ��
��
��PE��![]() PB��
PB��
��AP��AB��
���APB����B��
��OE��AP��
���OEB����APB��
���OEB����B��
��OE��OB��2����3+��B��180����
��AQ��PB��
���OAQ+��B��180����
���OAQ����3��
�ߡ�AOP����1+��QOP����2+��B����QOP����B��
���1����2��
���OAQ�ס�PEO��
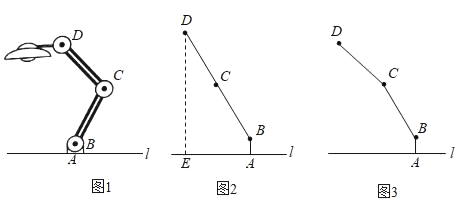
��![]() ������
������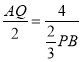 ��
��
����ã�AQPB��12��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1Ϊ������ˮƽ����l�ϵ�̨�ƣ������ĸ�ABΪ5cm�����Ⱦ�Ϊ20cm������BC��CD��ABʼ����ͬһƽ���ϣ�
��1��ת������BC��CD��ʹ��BCD��ƽ�ǣ���ABC��150�㣬��ͼ2�������˶˵�D������l�ĸ߶�DE��
��2������1���е�����CD���Ƶ�C��ʱ����ת����������֣���ͼ3������BCD��150��ʱ̨�ƹ�����ѣ����ʱ���˶˵�D������l�ĸ߶ȱ�ԭ�������˶������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪ij�����κ�����ͼ����A��1��2����B��2����1����C��4����1�����Ҹö��κ�������Сֵ�ǩ�2��

��1������ͼ������ú���ͼ��������������㣬������ͼ��
��2������ö��κ����Ľ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AN����һ��B��AB��5��tan��MAN��![]() ����C�ӵ�A������ÿ��3����λ���ȵ��ٶ�������AN�˶�������C��CD��AN������AM�ڵ�D��������CD��ȡ��F��ʹ��CF��CB������AF�����C���˶�ʱ����t���룩��t��0����
����C�ӵ�A������ÿ��3����λ���ȵ��ٶ�������AN�˶�������C��CD��AN������AM�ڵ�D��������CD��ȡ��F��ʹ��CF��CB������AF�����C���˶�ʱ����t���룩��t��0����
��1������C�ڵ�B�Ҳ�ʱ����AD��DF�ij������ú�t�Ĵ���ʽ��ʾ��
��2������BD������BCD�����ΪSƽ����λ����S��t֮��ĺ�����ϵʽ��
��3������AFD����Գ�ͼ��ʱ��ֱ��д��t��ֵ��
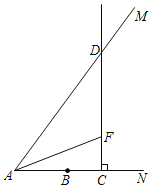
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������й���ͳ��ѧ����Ҫ���������춨���й���ͳ��ѧ�Ļ�����������о��ھš����ɡ�������Ҫ�������Բ�������Ϊ���ĵ�ֱ��������������Ĺ�ϵ�����м��أ����������������������ϱ����������п�����������һʮ������ľ���ʣ������ż��β�����ľ�������ģ�����ͼ������һ��������С�����������ǽ��7�����ϱ����ǽ��9��������ǽ���о���һ�������߳�����15�ﴦ�пô��������߳����Ŷ��ٲ�ǡ�����������������(ע��1�300��)��ļ������ǣ�������________������ľ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BDΪ��ABC���Բ��O��ֱ�����ҡ�BAE����C��
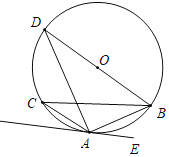
��1����֤��AE���O�����ڵ�A��
��2����AE��BC��BC��8��AB��2![]() �����O�İ뾶��
�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺����֪�����ı��ε�һ���Խ��߰�����ı��ηֳ������������Σ�������������������ƣ���ȫ�ȣ������ǾͰ������Խ��߽�������ı��ε������ƶԽ�������
���⣺��1����ͼ1����֪Rt��ABC�������������У�����ֻ���̶ȵ�ֱ�����������ҵ�һ��D��ʹ�ı���ABCD����ACΪ�����ƶԽ��������ı��Σ�������ͼ�ۼ����ҳ�3�����ɣ���
��2����ͼ2�����ı���ABCD�У���ABC��80������ADC��140�����Խ���BDƽ�֡�ABC����֤��BD���ı���ABCD�������ƶԽ�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ө�3����2����1��0��1��2��3���߸����У������ȡһ������Ϊm������mʹ����x�ķ�ʽ����![]() ��1��
��1��![]() �Ľ��ǷǸ�������ʹ�ö��κ���y����m��2��x2+2x+1��ͼ����x���н��㣬��ô������������m֮���ǣ�������
�Ľ��ǷǸ�������ʹ�ö��κ���y����m��2��x2+2x+1��ͼ����x���н��㣬��ô������������m֮���ǣ�������
A.4B.3C.2D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() .
.
��1�����˺���ͼ����![]() ��ֻ��һ�����㣬��д��
��ֻ��һ�����㣬��д��![]() ��
��![]() ����Ĺ�ϵʽ.
����Ĺ�ϵʽ.
��2����![]() ����
����![]() ��
��![]() ��
��![]() �Ǹú���ͼ���ϵ�3���㣬�ԱȽ�
�Ǹú���ͼ���ϵ�3���㣬�ԱȽ�![]() ��
��![]() ��
��![]() �Ĵ�С.
�Ĵ�С.
��3����![]() ����
����![]() ʱ������
ʱ������![]() ��
��![]() �������������
�������������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com