
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.
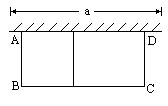
(1)如果要围成面积为45m2的花圃,AB的长是多少米?
(2)能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
|
[答案]设花圃的宽AB为x m,面积为y m2,则y=x(24-3x)=-3x2+24x. (1)当y=45时,-3x2+24x=45,即x2-8x+15=0,解得:x1=3,x2=5. 当 x=3时,BC=24-3x=24-9=15>10,故不合题意,舍去,从而x=5,即AB的长是5m.(2)能围成.y=-3x2+24x=-3(x-4)2+48. 由 0<24-3x=BC≤10,得故当 x=[剖析]先设出AB的长为x m,再用含x的代数式表示花圃的长BC,从而建立面积y与x的函数关系式.由于函数图像的对称轴为x=4,且开口向下, |
|
[拓展延伸] 解决此类问题的基本思路是: (1)理解问题;(2)分析问题中的变量和常量,以及它们之间的关系;(3)用数学的方式表示它们之间的关系;(4)做数学求解;(5)检验结果的合理性. |


科目:初中数学 来源: 题型:
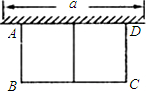 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花辅,设花圃的宽AB为x(m),面积为y(m2),求:
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花辅,设花圃的宽AB为x(m),面积为y(m2),求:查看答案和解析>>
科目:初中数学 来源: 题型:
 20、如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm.
20、如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm.查看答案和解析>>
科目:初中数学 来源: 题型:
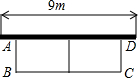 长方形养鸡场.设养鸡场的长BC为xm,面积为ym2.
长方形养鸡场.设养鸡场的长BC为xm,面积为ym2.查看答案和解析>>
科目:初中数学 来源:2013届安徽省定远中学九年级第一次素质考试数学试卷(带解析) 题型:解答题
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为xm,面积为Sm2.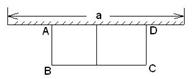
(1)求S与x的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45 m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年安徽省九年级第一次素质考试数学试卷(解析版) 题型:解答题
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为xm,面积为Sm2.
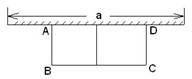
(1)求S与x的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45 m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com