练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．若$\frac{a}{b}$=$\frac{c}{d}$=3（2b-3d≠0），则$\frac{2a-3c}{2b-3d}$=3．

    分析 先将两个比例整理，再根据等比性质求解即可．

    解答 解：∵$\frac{a}{b}$=$\frac{c}{d}$=3，
    ∴$\frac{2a}{2b}$=$\frac{3c}{3d}$=3，
    ∴$\frac{2a-3c}{2b-3d}$=$\frac{2a}{2b}$=3．
    故答案为：3．

    点评 本题考查了比例的性质，主要利用了等比性质，需熟记．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．在等腰△ABC中，
    （1）如图1，若△ABC为等边三角形，D为线段BC中点，线段AD关于直线AB的对称线      段为线段AE，连接DE，则∠BDE的度数为30°；
    （2）若△ABC为等边三角形，点D为线段BC上一动点（不与B，C重合），连接AD并将   线段AD绕点D逆时针旋转60°得到线段DE，连接BE．
    ①根据题意在图2中补全图形；
    ②小玉通过观察、验证，提出猜测：在点D运动的过程中，恒有CD=BE．经过与同学们的充分讨论，形成了几种证明的思路：
    思路1：要证明CD=BE，只需要连接AE，并证明△ADC≌△AEB；
    思路2：要证明CD=BE，只需要过点D作DF∥AB，交AC于F，证明△ADF≌△DEB；
    思路3：要证明CD=BE，只需要延长CB至点G，使得BG=CD，证明△ADC≌△DEG；
    …
    请参考以上思路，帮助小玉证明CD=BE．（只需要用一种方法证明即可）
    （3）小玉的发现启发了小明：如图3，若AB=AC=kBC，AD=kDE，且∠ADE=∠C，此时小明发现BE，BD，AC三者之间满足一定的数量关系，这个数量关系是k（BE+BD）=AC．（直接给出结论无须证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．已知纽约比北京时间晚13个小时，如果北京时间是4月22日早上9：00点，此时纽约的时间为4月21 日20：00点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．把下列各数填在相应的大括号里：
    +5，-|-2|，-3，0，3$\frac{1}{2}$，-1.414，17，-$\frac{2}{3}$，（-1）2
    正整数：{+5，17，（-1）2…}；
    整数：{+5，-|-2|，-3，0，17，（-1）2…}；
    负分数：{3$\frac{1}{2}$，-1.414，-$\frac{2}{3}$…}；
    正有理数：{+5，3$\frac{1}{2}$，17，（-1）2…}．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如图，在平面直角坐标系xOy中，?OABC的边OC在x轴上，A（1，4）、C（3，0）点D在AB上，D（3，4），过点D的直线l平分?OABC的面积，现将l绕点A逆时针旋转90°得直线l′，则直线l′的函数解析式为（　　）
    A．y=-2x+6B．y=-2x+6.5C．$y=-\frac{1}{2}x+\frac{5}{2}$D．$y=-\frac{1}{2}x+\frac{13}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

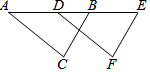    19．平移不改变图形的形状和大小．如图，△DEF是由△ABC经过平移得到的，若∠C=80°，∠A=33°，则∠EDF=33°，∠DEF=67°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

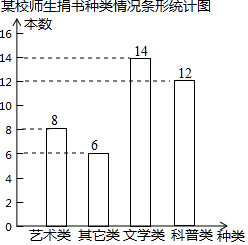    6．为了解某校师生捐书情况，随机调查了部分师生，根据调查结果绘制了如图所示的统计图．若该校共有师生1000人，则捐文学类书籍的师生约有350人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．（1）探究发现
    数学活动课上，小明说“若直线y=2x-1向左平移3个单位，你能求平移后所得直线所对应函数表达式吗？”
    经过一番讨论，小组成员展示了他们的解答过程：
    在直线y=2x-1上任取点A（0，-1），
    向左平移3个单位得到点A′（-3，-1）
    设向左平移3个单位后所得直线所对应的函数表达式为y=2x+n．
    因为y=2x+n过点A′（-3，-1），
    所以-6+n=-1，
    所以n=5，
    填空：所以平移后所得直线所对应函数表达式为y=2x+5
    （2）类比运用
    已知直线y=2x-1，求它关于x轴对称的直线所对应的函数表达式；
    （3）拓展运用
    将直线y=2x-1绕原点顺时针旋转90°，请直接写出：旋转后所得直线所对应的函数表达式y=-$\frac{1}{2}$x-$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．在平面直角坐标系xOy中，二次函数y=mx2-（2m+1）x+m-5的图象与x轴有两个公共点．
    （1）求m的取值范围；
    （2）若m取满足条件的最小的整数，
    ①写出这个二次函数的解析式；
    ②当n≤x≤1时，函数值y的取值范围是-6≤y≤4-n，求n的值；
    ③将此二次函数平移，使平移后的图象经过原点O．设平移后的图象对应的函数表达式为y=a（x-h）2+k，当x＜2时，y随x的增大而减小，求k的取值范围．

    查看答案和解析>>

    同步练习册答案