
| 成本 (单位:万元/亩) | 销售额(单位:万元/亩) | |
| 郁金香 | 2.4 | 3 |
| 玫瑰 | 2 | 2.5 |
分析 (1)根据种植郁金香和玫瑰两种花卉共30亩,可得出种植玫瑰30-x亩,再根据“总收益=郁金香每亩收益×种植亩数+玫瑰每亩收益×种植亩数”即可得出y关于x的函数关系式;
(2)根据“投入成本=郁金香每亩成本×种植亩数+玫瑰每亩成本×种植亩数”以及总成本不超过70万元,可得出关于x的一元一次不等式,解不等式即可得出x的取值范围,再根据一次函数的性质即可解决最值问题;
(3)设原计划每次运送化肥mkg,实际每次运送1.25mkg,根据原计划运送次数比实际次数多1,可得出关于m的分式方程,解分式方程即可得出结论.
解答 解:(1)设种植郁金香x亩,总收益为y万元,则种植玫瑰30-x亩,
由题意得:y=(3-2.4)x+(2.5-2)(30-x)=0.1x+15(0≤x≤30).
(2)由题意知:2.4x+2(30-x)≤70,
解得:x≤25.
∵y=0.1x+15中k=0.1>0,
∴y随x的增大而增大,
∴当x=25时,所获总收益最大,此时种植郁金香25亩,种植玫瑰5亩.
(3)设原计划每次运送化肥mkg,实际每次运送1.25mkg,
需要运送的化肥总量是400×25+600×5=13000(kg),
由题意可得:$\frac{13000}{m}$-$\frac{13000}{1.25m}$=1,
解得:m=2600,
经检验m=2600是原方程得解.
答:基地原计划每次运送化肥2600kg.
点评 本题考查了一次函数的应用、解一元一次不等式以及分式方程的应用,解题的关键是:(1)根据数量关系找出y关于x的函数关系式;(2)根据一次函数的性质解决最值问题;(3)根据数量关系得出分式方程.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出方程(方程组或函数关系式)是关键.


科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
如图,在?ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
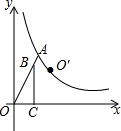 如图,点A是双曲线y=$\frac{k}{x}$(x>0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,$\frac{OB}{OA}$=$\frac{\sqrt{2}}{2}$.
如图,点A是双曲线y=$\frac{k}{x}$(x>0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,$\frac{OB}{OA}$=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com