
【题目】如图,在⊙O中,AB为直径,点M为AB延长线上的一点,MC与⊙O相切于点C,圆周上有另一点D与点C分居直径AB两侧,且使得MC=MD=AC,连接AD.现有下列结论:①MD与⊙O相切;②四边形ACMD是菱形;③AB=MO;④∠ADM=120°,其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
【答案】A
【解析】
如图,连接CO,DO,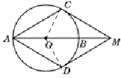
∵MC与⊙O相切于点C,
∴∠MCO=90°,
在△MCO与△MDO中,
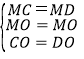 ,
,
∴△MCO≌△MDO(SSS),
∴∠MCO=∠MDO=90°,∠CMO=∠DMO,
∴MD与⊙O相切,故①正确;
在△ACM与△ADM中,
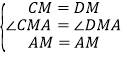 ,
,
∴△ACM≌△ADM(SAS),
∴AC=AD,
∴MC=MD=AC=AD,
∴四边形ACMD是菱形,故②正确;
如图连接BC,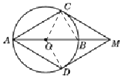
∵AC=MC,
∴∠CAB=∠CMO,
又∵AB为⊙O的直径,
∴∠ACB=90°,
在△ACB与△MCO中,
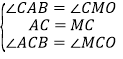 ,
,
∴△ACB≌△MCO(SAS),
∴AB=MO,故③正确;
∵△ACB≌△MCO,
∴BC=OC,
∴BC=OC=OB,
∴∠COB=60°,
∵∠MCO=90°,
∴∠CMO=30°,
又∵四边形ACMD是菱形,
∴∠CMD=60°,
∴∠ADM=120°,故④正确;
故正确的有4个.
故选A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知AB,CD都是![]() 的直径,连接DB,过点C的切线交DB的延长线于点E.
的直径,连接DB,过点C的切线交DB的延长线于点E.
![]() 如图1,求证:
如图1,求证:![]() ;
;
![]() 如图2,过点A作
如图2,过点A作![]() 交EC的延长线于点F,过点D作
交EC的延长线于点F,过点D作![]() ,垂足为点G,求证:
,垂足为点G,求证:![]() ;
;
![]() 如图3,在
如图3,在![]() 的条件下,当
的条件下,当![]() 时,在
时,在![]() 外取一点H,连接CH、DH分别交
外取一点H,连接CH、DH分别交![]() 于点M、N,且
于点M、N,且![]() ,点P在HD的延长线上,连接PO并延长交CM于点Q,若
,点P在HD的延长线上,连接PO并延长交CM于点Q,若![]() ,
,![]() ,
,![]() ,求线段HM的长.
,求线段HM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次,掷第一次,将朝上一面的点数记为![]() ,掷第二次,将朝上一面的点数记为
,掷第二次,将朝上一面的点数记为![]() ,则点(
,则点(![]() )落在直线
)落在直线![]() 上的概率为:
上的概率为:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.
设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).
(1)请分别写出y1,y2与x之间的函数表达式.
(2)若小亮一年内来此游泳馆的次数为15次,选择哪种方式比较划算?
(3)若小亮计划拿出1400元用于在此游泳馆游泳,采用哪种付费方式更划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润![]() (元)与国内销售数量
(元)与国内销售数量![]() (千件)的关系为:
(千件)的关系为: 若在国外销售,平均每件产品的利润
若在国外销售,平均每件产品的利润![]() (元)与国外的销售数量t(千件)的关系为:
(元)与国外的销售数量t(千件)的关系为:
(1)用![]() 的代数式表示t为:t= ;当0<
的代数式表示t为:t= ;当0<![]() ≤4时,
≤4时,![]() 与
与![]() 的函数关系式为:
的函数关系式为:![]() = ;当4≤
= ;当4≤![]() < 时,
< 时,![]() =100;
=100;
(2)求每年该公司销售这种健身产品的总利润W(千元)与国内的销售数量x(千件)的函数关系式,并指出x的取值范围;
(3)该公司每年国内、国外的销量各为多少时,可使公司每年的总利润最大?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-5,1),B(-1,1),C(-4,3).
(1)若△A1B1C1与△ABC关于y轴对称,点A,B,C的对应点分别为A1,B1,C1,请画出△A1B1C1并写出A1,B1,C1的坐标;
(2)若点P为平面内不与C重合的一点,△PAB与△ABC全等,请写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )

A. 40°B. 50°C. 60°D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
![]() Ⅰ
Ⅰ![]() 直线
直线![]() 与x轴夹成的锐角为______度;直线
与x轴夹成的锐角为______度;直线![]() 与x轴夹成的锐角为______度;直线
与x轴夹成的锐角为______度;直线![]() 与x轴夹成的锐角为______度;
与x轴夹成的锐角为______度;
![]() Ⅱ
Ⅱ![]() 设直线
设直线![]() 与x轴夹成的锐角为
与x轴夹成的锐角为![]() ,试用
,试用![]() 的三角函数表示k,并给予证明.
的三角函数表示k,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com