
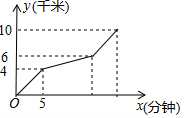
 如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )
如图,小磊老师从甲地去往10千米的乙地,开始以一定的速度行驶,之后由于道路维修,速度变为原来的四分之一,过了维修道路后又变为原来的速度到达乙地.设小磊老师行驶的时间为x(分钟),行驶的路程为y(千米),图中的折线表示y与x之间的函数关系,则小磊老师从甲地到达乙地所用的时间是( )| A. | 15分钟 | B. | 20分钟 | C. | 25分钟 | D. | 30分钟 |
科目:初中数学 来源: 题型:填空题
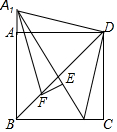 如图,在正方形ABCD中,点C1在边BC上,将△C1CD绕点D顺时针旋转90°得到△A1AD.A1F平分∠BA1C1,交BD于点F,过点F作FE⊥A1C1,垂足为E,当A1E=3,C1E=2时,则BD的长为$\frac{7\sqrt{2}}{2}$.
如图,在正方形ABCD中,点C1在边BC上,将△C1CD绕点D顺时针旋转90°得到△A1AD.A1F平分∠BA1C1,交BD于点F,过点F作FE⊥A1C1,垂足为E,当A1E=3,C1E=2时,则BD的长为$\frac{7\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.
如图,四边形ABCD为平行四边形,E为BC的中点,连接AE并延长交DC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
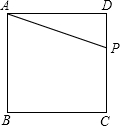 如图,正方形ABCD的边长为4cm,点P从点D出发,沿边DC,CB,BA运动(点P与A重合时停止运动).设P点运动的速度为1cm/s.
如图,正方形ABCD的边长为4cm,点P从点D出发,沿边DC,CB,BA运动(点P与A重合时停止运动).设P点运动的速度为1cm/s.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
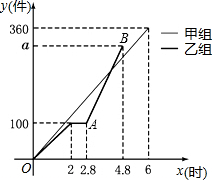 甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.下列说法:①甲组加工零件的总量比乙组加工零件总量多;②乙组加工零件总量的a值是300件;③甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,经过3小时恰好装满第1箱④经过4.5小时甲、乙两组加工出的零件数相同,其中正确的个数为( )
甲、乙两组工人同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.下列说法:①甲组加工零件的总量比乙组加工零件总量多;②乙组加工零件总量的a值是300件;③甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,经过3小时恰好装满第1箱④经过4.5小时甲、乙两组加工出的零件数相同,其中正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
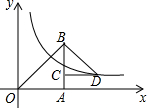 如图,在平面直角坐标系中,点A在x轴的正半轴上,点B在第一象限,点C在线段AB上,点D在AB的右侧,△OAB和△BCD都是等腰直角三角形,∠OAB=∠BCD=90°,若函数y=$\frac{6}{x}$(x>0)的图象经过点D,则△OAB与△BCD的面积之差为( )
如图,在平面直角坐标系中,点A在x轴的正半轴上,点B在第一象限,点C在线段AB上,点D在AB的右侧,△OAB和△BCD都是等腰直角三角形,∠OAB=∠BCD=90°,若函数y=$\frac{6}{x}$(x>0)的图象经过点D,则△OAB与△BCD的面积之差为( )| A. | 12 | B. | 6 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com