
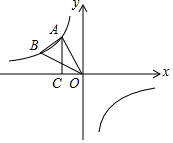
 如图,点A,点B在反比例函数y=$\frac{k}{x}$的图象上,且点A,点B的横坐标分别为a,2a(a<0),AC⊥x轴于点C,且S△AOC=2.
如图,点A,点B在反比例函数y=$\frac{k}{x}$的图象上,且点A,点B的横坐标分别为a,2a(a<0),AC⊥x轴于点C,且S△AOC=2.分析 (1)直接根据反比例函数系数k的几何意义即可得出结论;
(2)先判断出两点所在象限,再由反比例函数的增减性即可得出结论;
(3)过点B作BE⊥x轴,交x轴于E点,通过分割面积法S△AOB=S△AOC+S梯形-S△BOE求得.
解答 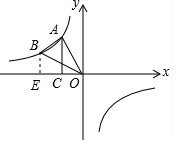 解:(1)∵AC⊥x轴于点C,且S△AOC=2,
解:(1)∵AC⊥x轴于点C,且S△AOC=2,
∴k=-4,
∴这个反比例函数的解析式为y=-$\frac{4}{x}$;
(2)∵a<0,
∴-a>0,
∴-a<-2a,
∴点(-a,y1)和点(-2a,y2)在第四象限.
∵k=-4<0,
∴在每一象限内y随x的增大而增大,
∴y1<y2;
(3)连接AB,过点B作BE⊥x轴,
S△AOC=S△BOE=2,
∴A(a,$\frac{4}{a}$),B(2a,$\frac{2}{a}$);
S梯形ACEB=$\frac{1}{2}$(-$\frac{4}{a}$-$\frac{2}{a}$)×(-2a+a)=3,
∴S△AOB=S△AOC+S梯形ACEB-S△BOE=3.
点评 此题考查的待定系数法求反比例函数的解析式,涉及到函数性质的应用和图形的分割转化思想,同学们要熟练掌握这类题型.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
| 里程(单位:km) | 收费(单位:元) |
| 3km以下(含3km) | 8.0 |
| 3km以上(每增加1km) | 1.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>4 | B. | 0<a<4 | C. | a>2 | D. | 0<a<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
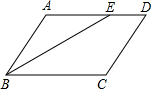 如图,在四边形ABCD中,BE平分∠ABC,∠AEB=∠ABE.
如图,在四边形ABCD中,BE平分∠ABC,∠AEB=∠ABE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com