
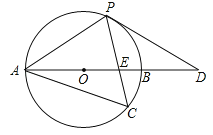
【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=4,求CECP的值.
【答案】(1)PD是⊙O的切线;(2)8.
【解析】
试题分析:(1)连结OP,根据圆周角定理可得∠AOP=2∠ACP=120°,然后计算出∠PAD和∠D的度数,进而可得∠OPD=90°,从而证明PD是⊙O的切线;
(2)连结BC,首先求出∠CAB=∠ABC=∠APC=45°,然后可得AC长,再证明△CAE∽△CPA,进而可得![]() ,然后可得CECP的值.
,然后可得CECP的值.
试题解析:(1)如图,PD是⊙O的切线.
证明如下:
连结OP,∵∠ACP=60°,∴∠AOP=120°,∵OA=OP,∴∠OAP=∠OPA=30°,∵PA=PD,∴∠PAO=∠D=30°,∴∠OPD=90°,∴PD是⊙O的切线.
(2)连结BC,∵AB是⊙O的直径,∴∠ACB=90°,又∵C为弧AB的中点,∴∠CAB=∠ABC=∠APC=45°,∵AB=4,AC=Absin45°=![]() .∵∠C=∠C,∠CAB=∠APC,∴△CAE∽△CPA,∴
.∵∠C=∠C,∠CAB=∠APC,∴△CAE∽△CPA,∴![]() ,∴CPCE=CA2=(
,∴CPCE=CA2=(![]() )2=8.
)2=8.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】夏季来临,商场准备购进甲、乙两种空调![]() 已知甲种空调每台进价比乙种空调多500元,用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同
已知甲种空调每台进价比乙种空调多500元,用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同![]() 请解答下列问题:
请解答下列问题:
![]() 求甲、乙两种空调每台的进价;
求甲、乙两种空调每台的进价;
![]() 若甲种空调每台售价2500元,乙种空调每台售价1800元,商场欲同时购进两种空调20台,且全部售出,请写出所获利润
若甲种空调每台售价2500元,乙种空调每台售价1800元,商场欲同时购进两种空调20台,且全部售出,请写出所获利润![]() 元
元![]() 与甲种空调
与甲种空调![]() 台
台![]() 之间的函数关系式;
之间的函数关系式;
![]() 在
在![]() 的条件下,若商场计划用不超过36000元购进空调,且甲种空调至少购进10台,并将所获得的最大利润全部用于为某敬老院购买1100元
的条件下,若商场计划用不超过36000元购进空调,且甲种空调至少购进10台,并将所获得的最大利润全部用于为某敬老院购买1100元![]() 台的A型按摩器和700元
台的A型按摩器和700元![]() 台的B型按摩器
台的B型按摩器![]() 直接写出购买按摩器的方案.
直接写出购买按摩器的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中,一定正确的个数是( )
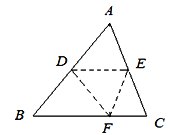
①△BDF是等腰三角形;
②DE=![]() BC;
BC;
③四边形ADFE是菱形;
④∠BDF+∠FEC=2∠A.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是( )

A. 四边形CEDF是平行四边形
B. 当![]() 时,四边形CEDF是矩形
时,四边形CEDF是矩形
C. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
D. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备为七年级学生开设![]() 共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
共6门选修课,选取了若干学生进行了我最喜欢的一门选修课调查,将调查结果绘制成了如图所示的统计图表(不完整).
选修课 |
|
|
|
|
|
|
人数 | 40 | 60 | 100 |
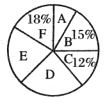
下列说法不正确的是( )
A.这次被调查的学生人数为400人B.![]() 对应扇形的圆心角为
对应扇形的圆心角为![]()
C.喜欢选修课![]() 的人数为72人D.喜欢选修课
的人数为72人D.喜欢选修课![]() 的人数最少
的人数最少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将函数 y=2x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方,所得的折线是函数y=![]() (b为常数)的图象,若该图象在直线y=1下方的点的横坐标x满足0<x<3,则 b的取值范围为( )
(b为常数)的图象,若该图象在直线y=1下方的点的横坐标x满足0<x<3,则 b的取值范围为( )
A.-5≤b≤-1B.-3≤b≤-1C.-2≤b≤0D.-3≤b≤0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A. “明天降雨的概率是80%”表示明天有80%的时间都在降雨
B. “抛一枚硬币正面朝上的概率为![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C. “彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D. “抛一枚正方体骰子,朝上的点数为2的概率为![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
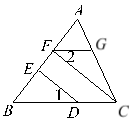
证明:∵CF⊥AB,DE⊥AB (已知)
∴∠BED=90°,∠BFC=90°( )
∴∠BED=∠BFC ( )
∴ED∥FC ( )
∴∠1=∠BCF ( )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( )
∴FG∥BC ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com