
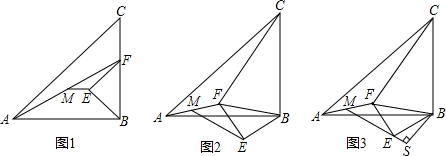
分析 (1)①延长EF交AB于D,如图1,则可判断△BED和△BEF为全等的等腰直角三角形,所以△BED为所作;
②先证明ME为△FAD的中位线得到AD=2ME,再利用等腰直角三角形的性质和等量代换得到AD=CF,于是有CF=2ME;
(2)延长FE到点G,使EG=EF,如图2,连结AG、BG,先证明ME为△FAG的中位线得到AG=2ME,然后证明△ABG≌△CBF得到AG=CF,所以CF=2ME;
(4)延长FE到点G,使EG=EF,如图3,连结AG、BG,作FH⊥ME于H,交AG于L,延长BS交AG于K,利用△ABG≌△CBF得到AG=CF=10,S△ABG=S△CBF,再证明△FEH≌△EBS得到FH=ES=2,接着利用ME为△FAG的中位线得到FH=HL=2,ME∥AG,于是判断四边形HLKS为矩形得到SK=HL=2,则BK=6,则可计算出S△ABG,从而得到S△CBF的值,然后利用勾股定理计算出EF,则可计算出S△BEF,最后利用S四边形CFEB=S△BCF+S△BEF进行计算即可.
解答 (1)解:①延长EF交AB于D,如图1,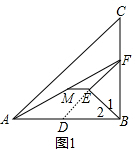
∵等腰直角△ABC和等腰直角△BEF,∠ABC=∠BEF=90°,
∴∠1=∠BFE=45°,
∴∠2=∠BDE=45°,
∴EF=ED=BE,
即BE垂直平分DF,
∴△BED与△BEF关于直线BE对称,
即△BED为所作;
②证明∵M点为AF的中点,
而EF=ED,
∴ME为△FAD的中位线,
∴AD=2ME,
∵BD=BF,BA=BC,
∴AD=CF,
∴CF=2ME;
(2)解:(1)中的结论②仍成立.理由如下:
延长FE到点G,使EG=EF,如图2,连结AG、BG,
∵M点为AF的中点,
而EF=EG,
∴ME为△FAG的中位线,
∴AG=2ME,
∵△BEF为等腰直角三角形,
∴∠BEF=90°,BE=EF,
而EF=EG,
∴△BEG为等腰直角三角形,
∴∠BGE=∠EBG=45°,
∴△FBG为等腰直角三角形,
∴BF=BG,∠FBG=90°,
∵∠ABG+∠ABF=90°,∠CBF+∠ABF=90°,
∴∠ABG=∠CBF,
在△ABG和△CBF中
$\left\{\begin{array}{l}{BA=BC}\\{∠ABG=∠CBF}\\{BG=BF}\end{array}\right.$,
∴△ABG≌△CBF,
∴AG=CF,
∴CF=2ME;
(4)延长FE到点G,使EG=EF,如图3,连结AG、BG,作FH⊥ME于H,交AG于L,延长BS交AG于K,
由(3)得△ABG≌△CBF,
∴AG=CF=10,S△ABG=S△CBF,
∵∠FEH+∠BES=90°,∠EBS+∠BES=90°,
∴∠FEH=∠EBS,
在△FEH和△EBS中
$\left\{\begin{array}{l}{∠FHE=∠BSE}\\{∠FEH=∠EBS}\\{FE=EB}\end{array}\right.$,
∴△FEH≌△EBS,
∴FH=ES=2,
∵ME为△FAG的中位线,
∴FH=HL=2,ME∥AG,
易得四边形HLKS为矩形,
∴SK=HL=2,
∴BK=BS+SK=4+2=6,
∴S△ABG=$\frac{1}{2}$•10•6=30,
∴S△CBF=30,
在Rt△BES中,BE=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴S△BEF=$\frac{1}{2}$•2$\sqrt{5}$•2$\sqrt{5}$=10,
∴S四边形CFEB=S△BCF+S△BEF=30+10=40.
故答案为40.
点评 本题考查了几何变换综合题:熟练掌握旋转的性质和等腰直角三角形的性质;利用线段中点构建三角形中位线得到线段之间的位置关系与数量关系;会利用全等三角形的知识解决线段相等的问题.


科目:初中数学 来源: 题型:填空题
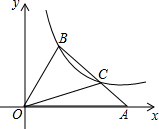 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,则△OAB的面积等于3.
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,OC是△OAB的中线,点B,C在反比例函数y=$\frac{2}{x}$(x>0)的图象上,则△OAB的面积等于3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
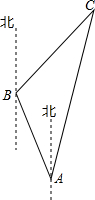 为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查,一测量船在A岛测得B岛在北偏西30°,C岛在北偏东15°,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离($\sqrt{6}$≈2.45,结果保留到整数)
为有效开发海洋资源,保护海洋权益,我国对南海诸岛进行了全面调查,一测量船在A岛测得B岛在北偏西30°,C岛在北偏东15°,航行100海里到达B岛,在B岛测得C岛在北偏东45°,求B,C两岛及A,C两岛的距离($\sqrt{6}$≈2.45,结果保留到整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com