
【题目】某企业设计了一款工艺品,每件成本40元,出于营销考虑,要求每件售价不得低于40元,但物价部门要求每件售价不得高于60元.据市场调查,销售单价是50元时,每天的销售量是100件,而销售单价每涨1元,每天就少售出2件,设单价上涨![]() 元
元![]() .
.
(1)求当![]() 为多少时每天的利润是1350元?
为多少时每天的利润是1350元?
(2)设每天的销售利润为![]() ,求销售单价为多少元时,每天利润最大?最大利润是多少?
,求销售单价为多少元时,每天利润最大?最大利润是多少?
科目:初中数学 来源: 题型:
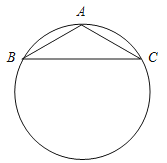
【题目】如图,已知弧上的三点A、B、C,连结AB,AC,BC.
(1)用尺规作图法找出![]() 所在圆的圆心.(保留作图痕迹,不写作法)
所在圆的圆心.(保留作图痕迹,不写作法)
(2)若A是![]() 的中点,BC=8cm,AB=5cm.求圆的半径
的中点,BC=8cm,AB=5cm.求圆的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动手操作:(不要求写作法和证明,只保留作图痕迹)
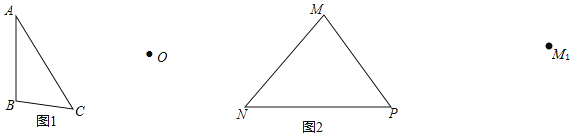
(1)如图![]() 所示,以点
所示,以点![]() 为对称中心,画出与
为对称中心,画出与![]() 成中心对称的图形
成中心对称的图形![]() .
.
(2)如图![]() 所示,将
所示,将![]() 绕点
绕点![]() 旋转后,顶点
旋转后,顶点![]() 旋转到了
旋转到了![]() 处,试画出旋转后的
处,试画出旋转后的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线![]() 经过点
经过点![]() 、
、![]() 、
、![]() ,已知点
,已知点![]() ,
,![]() ,且
,且![]() ,点
,点![]() 为抛物线上一点(异于
为抛物线上一点(异于![]() ).
).
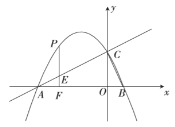
(1)求抛物线和直线![]() 的表达式.
的表达式.
(2)若点![]() 是直线
是直线![]() 上方抛物线上的点,过点
上方抛物线上的点,过点![]() 作
作![]() ,与
,与![]() 交于点
交于点![]() ,垂足为
,垂足为![]() .当
.当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(3)若点![]() 为
为![]() 轴上一动点,是否存在点
轴上一动点,是否存在点![]() ,使得由
,使得由![]() ,
,![]() ,
,![]() ,
,![]() 四点组成的四边形为平行四边形?若存在,直接写出点
四点组成的四边形为平行四边形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]()
![]() ,
,![]()
![]() ,将直线
,将直线![]() 平移与双曲线
平移与双曲线![]() 在第一象限的图象交于
在第一象限的图象交于![]() 、
、![]() 两点.
两点.
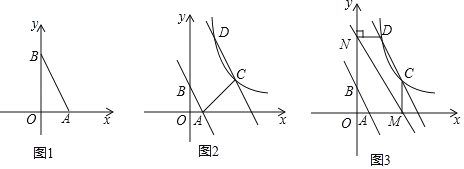
(1)如图1,将![]() 绕
绕![]() 逆时针旋转
逆时针旋转![]() 得
得![]() 与
与![]() 对应,
对应,![]() 与
与![]() 对应),在图1中画出旋转后的图形并直接写出
对应),在图1中画出旋转后的图形并直接写出![]() 、
、![]() 坐标;
坐标;
(2)若![]() ,
,
①如图2,当![]() 时,求
时,求![]() 的值;
的值;
②如图3,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 有唯一公共点时,
有唯一公共点时,![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某学校七年级4个班共180人的体质健康情况,从各班分别抽取同样数量的男生和女生组成一个样本,如图是根据样本绘制的条形图和扇形图.
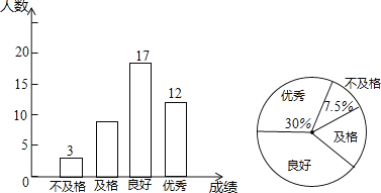
(1)本次抽查的样本容量是______.
(2)请补全条形图和扇形图中的百分数;
(3)请你估计全校七年级共有多少人优秀.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数的图像经过点(2,-3).
(1)求这个函数的表达式.
(2)点(-1,6),(3,2)是否在这个函数的图像上?
(3)这个函数的图像位于哪些象限?函数值y随自变量![]() 的增大如何变化?
的增大如何变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
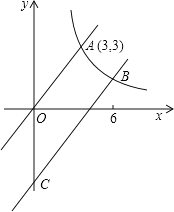
【题目】如图,直线OA与反比例函数的图象交于点A(3,3),向下平移直线OA,与反比例函数的图象交于点B(6,m)与y轴交于点C,
(1)求直线BC的解析式;
(2)求经过A、B、C三点的二次函数的解析式;
(3)设经过A、B、C三点的二次函数图象的顶点为D,对称轴与x轴的交点为E.
问:在二次函数的对称轴上是否存在一点P,使以O、E、P为顶点的三角形与△BCD相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com