
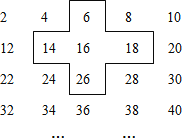
ЁОЬтФПЁПаЁУїЪЧИіАЎЖЏФдНюЕФЭЌбЇЃЌдкЗЂЯжНЬВФжаЕФгУЗНПђдкШеРњжавЦЖЏЕФЙцТЩКѓЃЌЭЛЗЂЦцЯыЃЌНЋСЌајЕФЕУЪ§2ЃЌ4ЃЌ6ЃЌ8ЃЌЁЃЌХХГЩШчЭМаЮЪНЃКВЂгУвЛИіЪЎзжаЮПђМмПђзЁЦфжаЕФЮхИіЪ§ЃЌЧыФузаЯИЙлВьЪЎзжаЮПђМмжаЕФЪ§зжЕФЙцТЩЃЌВЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧыФубЁдёЪЎзжПђжаФуЯВЛЖЕФШЮвтЮЛжУЕФвЛИіЪ§ЃЌНЋЦфЩшЮЊxЃЌВЂгУКЌxЕФДњЪ§ЪНБэЪОЪЎзжПђжаЮхИіЪ§ЕФКЭЃЎ
ЃЈ2ЃЉШєНЋЪЎзжПђЩЯЯТзѓгввЦЖЏЃЌПЩПђзЁСэЭтЕФЮхИіЪ§ЃЌЪдМфЃКЪЎзжПђФмЗёПђзЁКЭЕШгк2015ЕФЮхИіЪ§ЃЌШчФмЃЌЧыЧѓГіетЮхИіЪ§ЃЛШчВЛФмЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ5xЃЛЃЈ2ЃЉВЛФмЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЩшЪЎзжПђжажаМфЕФЪ§ЮЊxЃЌдђСэЭтЫФИіЪ§ЗжБ№ЮЊxЉ10ЃЌxЉ2ЃЌx+2ЃЌx+10ЃЌНЋЮхИіЪ§ЯрМгМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉгЩЮхИіЪ§жЎКЭЮЊ2015ЃЌПЩЕУГіЙигкxЕФвЛдЊвЛДЮЗНГЬЃЌНтжЎМДПЩЕУГіxЕФжЕЃЌгЩИУжЕВЛЮЊХМЪ§ПЩЕУГіЪЎзжПђВЛФмПђзЁКЭЕШгк2015ЕФЮхИіЪ§ЃЎ
НтЃКЃЈ1ЃЉЩшЪЎзжПђжажаМфЕФЪ§ЮЊxЃЌдђСэЭтЫФИіЪ§ЗжБ№ЮЊxЉ10ЃЌxЉ2ЃЌx+2ЃЌx+10ЃЌ
ЁрЪЎзжПђжаЮхИіЪ§ЕФКЭЃНЃЈxЉ10ЃЉ+ЃЈxЉ2ЃЉ+x+ЃЈx+2ЃЉ+ЃЈx+10ЃЉЃН5xЃЎ
ЃЈ2ЃЉВЛФмЃЌРэгЩШчЯТЃК
вРЬтвтЃЌЕУЃК5xЃН2015ЃЌ
НтЕУЃКxЃН403ЃЎ
ЁпЭМжаИїЪ§ОљЮЊХМЪ§ЃЌ
ЁрxЃН403ВЛЗћКЯЬтвтЃЌ
ЁрЪЎзжПђВЛФмПђзЁКЭЕШгк2015ЕФЮхИіЪ§ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
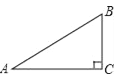
ЁОЬтФПЁПФГаЃМЦЛЎАбвЛПщНќЫЦгкжБНЧШ§НЧаЮЕФЗЯЕиПЊЗЂЮЊЩњЮядАЃЌШчЭМЫљЪОЃЌЁЯACB=90ЁуЃЌBC=60УзЃЌЁЯA=36ЁуЃЎ
ЃЈ1ЃЉШєШыПкДІEдкABБпЩЯЃЌЧвгыAЁЂBЕШОрРыЃЌЧѓCEЕФГЄЃЈОЋШЗЕНИіЮЛЃЉЃЛ
ЃЈ2ЃЉШєDЕудкABБпЩЯЃЌМЦЛЎбиЯпЖЮCDаовЛЬѕЫЎЧўЃЎвбжЊЫЎЧўЕФдьМлЮЊ50дЊ/УзЃЌЫЎЧўТЗЯпгІШчКЮЩшМЦВХФмЪЙдьМлзюЕЭЃЌЧѓГізюЕЭдьМлЃЎ
ЃЈЦфжаsin36Ёу=0.5878ЃЌcos36Ёу=0.8090ЃЌtan36Ёу=0.7265ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
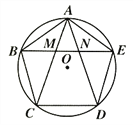
ЁОЬтФПЁПAЁЂBЁЂCЁЂDЫФИіГЕеОЕФЮЛжУШчЭМЫљЪОЃК

(1)ЧѓAЁЂDСНеОЕФОрРыЃЛ
(2)ЧѓCЁЂDСНеОЕФОрРыЃЛ
(3)БШНЯAЁЂCСНеОЕФОрРыгыBЁЂDСНеОЕФОрРыЃЌФФСНеОЕФОрРыИќДѓЃПДѓЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌвдACЮЊжБОЖзїЁбOЃЌНЛABгкDЃЌЙ§ЕуOзїOEЁЮABЃЌНЛBCгкEЃЎ
ЃЈ1ЃЉЧѓжЄЃКEDЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШчЙћЁбOЕФАыОЖЮЊ![]() ЃЌED=2ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЁЂAFЃЌЧѓЁїADFЕФУцЛ§ЃЎ
ЃЌED=2ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЁЂAFЃЌЧѓЁїADFЕФУцЛ§ЃЎ

ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЪзЯШСЌНгODЃЌгЩOEЁЮABЃЌИљОнЦНааЯпгыЕШбќШ§НЧаЮЕФаджЪЃЌвзжЄЕУ![]() Ёе
Ёе![]() МДПЩЕУ
МДПЩЕУ![]() ЃЌдђПЩжЄЕУ
ЃЌдђПЩжЄЕУ![]() ЮЊ
ЮЊ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉСЌНгCDЃЌИљОнжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЌМДПЩЕУ![]() РћгУЙДЙЩЖЈРэМДПЩЧѓЕУ
РћгУЙДЙЩЖЈРэМДПЩЧѓЕУ![]() ЕФГЄЃЌгжгЩOEЁЮABЃЌжЄЕУ
ЕФГЄЃЌгжгЩOEЁЮABЃЌжЄЕУ![]() ИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУ
ИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУ![]() ЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЕФжЊЪЖЃЌЧѓЕУ
ЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЕФжЊЪЖЃЌЧѓЕУ![]() гы
гы![]() ЕФГЄЃЌШЛКѓРћгУSЁїADF=SЬнаЮABEF-SЬнаЮDBEFЧѓЕУД№АИЃЎ
ЕФГЄЃЌШЛКѓРћгУSЁїADF=SЬнаЮABEF-SЬнаЮDBEFЧѓЕУД№АИЃЎ
ЪдЬтНтЮіЃК(1)жЄУїЃКСЌНгODЃЌ

ЁпOEЁЮABЃЌ
ЁрЁЯCOE=ЁЯCADЃЌЁЯEOD=ЁЯODAЃЌ
ЁпOA=OD,
ЁрЁЯOAD=ЁЯODAЃЌ
ЁрЁЯCOE=ЁЯDOEЃЌ
дкЁїCOEКЭЁїDOEжаЃЌ
 ЁрЁїCOEЁеЁїDOE(SAS)ЃЌ
ЁрЁїCOEЁеЁїDOE(SAS)ЃЌ
![]()
ЁрEDЁЭODЃЌ
ЁрEDЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
(2)СЌНгCDЃЌНЛOEгкMЃЌ
дкRtЁїODEжаЃЌ
ЁпOD=32ЃЌDE=2ЃЌ
![]()
ЁпOEЁЮABЃЌ
ЁрЁїCOEЁзЁїCABЃЌ
![]() ЁрAB=5ЃЌ
ЁрAB=5ЃЌ
ЁпACЪЧжБОЖЃЌ
![]()
![]()
![]()
![]()
ЁпEFЁЮABЃЌ
![]()
![]()
![]()
ЁрSЁїADF=SЬнаЮABEFSЬнаЮDBEF
![]()
ЁрЁїADFЕФУцЛ§ЮЊ![]()

ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
25
ЁОЬтФПЁПЁОЬтФПЁПвбжЊЃЌХзЮяЯпy=ax2+ax+bЃЈaЁй0ЃЉгыжБЯпy=2x+mгавЛИіЙЋЙВЕуMЃЈ1ЃЌ0ЃЉЃЌЧвaЃМbЃЎ
ЃЈ1ЃЉЧѓbгыaЕФЙиЯЕЪНКЭХзЮяЯпЕФЖЅЕуDзјБъЃЈгУaЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉжБЯпгыХзЮяЯпЕФСэЭтвЛИіНЛЕуМЧЮЊNЃЌЧѓЁїDMNЕФУцЛ§гыaЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉa=Љ1ЪБЃЌжБЯпy=Љ2xгыХзЮяЯпдкЕкЖўЯѓЯоНЛгкЕуGЃЌЕуGЁЂHЙигкдЕуЖдГЦЃЌЯжНЋЯпЖЮGHбиyжсЯђЩЯЦНвЦtИіЕЅЮЛЃЈtЃО0ЃЉЃЌШєЯпЖЮGHгыХзЮяЯпгаСНИіВЛЭЌЕФЙЋЙВЕуЃЌЪдЧѓtЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЮхБпаЮЕФБпГЄЮЊ2ЃЌСЌНгЖдНЧЯпADЁЂBEЁЂCEЃЌЯпЖЮADЗжБ№гыBEКЭCEЯрНЛгкЕуMЁЂNЃЌИјГіЯТСаНсТлЃКЂйЁЯAME=108ЁуЃЌЂкAN2=AMADЃЛЂлMN=3-![]() ЃЛЂмSЁїEBC=2
ЃЛЂмSЁїEBC=2![]() -1ЃЌЦфжае§ШЗЕФНсТлЪЧ_________ЃЈАбФуШЯЮЊе§ШЗНсТлЕФађКХЖМЬюЩЯЃЉЃЎ
-1ЃЌЦфжае§ШЗЕФНсТлЪЧ_________ЃЈАбФуШЯЮЊе§ШЗНсТлЕФађКХЖМЬюЩЯЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвджБЯпABЩЯвЛЕуOЮЊЖЫЕузїЩфЯп OCЃЌЪЙЁЯBOC=60ЁуЃЌНЋвЛИіжБНЧШ§НЧаЮЕФжБНЧЖЅЕуЗХдкЕуOДІЃЎЃЈзЂЃКЁЯDOE=90ЁуЃЉ
ЃЈ1ЃЉШчЭМ1ЃЌШєжБНЧШ§НЧАхDOEЕФвЛБпODЗХдкЩфЯпOBЩЯЃЌдђЁЯCOE= ЁуЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌНЋжБНЧШ§НЧАхDOEШЦЕуOФцЪБеыЗНЯђзЊЖЏЕНФГИіЮЛжУЃЌШєOEЧЁКУЦНЗжЁЯAOCЃЌЧыЫЕУїODЫљдкЩфЯпЪЧЁЯBOCЕФЦНЗжЯпЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌНЋШ§НЧАхDOEШЦЕуOФцЪБеызЊЖЏЕНФГИіЮЛжУЪБЃЌШєЧЁКУЁЯCOD= ![]() ЁЯAOEЃЌЧѓЁЯBODЕФЖШЪ§ЃП
ЁЯAOEЃЌЧѓЁЯBODЕФЖШЪ§ЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
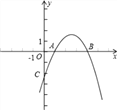
ЁОЬтФПЁПвбжЊЃЌХзЮяЯпy=ax2+bx-2гыxжсЕФСНИіНЛЕуЗжБ№ЮЊAЃЈ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌгыyжсЕФНЛЕуЮЊCЃЎ
ЃЈ1ЃЉЧѓГіХзЮяЯпЕФНтЮіЪНМАЕуCЕФзјБъЃЛ
ЃЈ2ЃЉЕуPЪЧдкжБЯпx=4гвВрЕФХзЮяЯпЩЯЕФвЛЖЏЕуЃЌЙ§PзїPMЁЭxжсЃЌДЙзуЮЊMЃЌЪЧЗёДцдкPЕуЃЌЪЙЕУвдAЃЌPЃЌMЮЊЖЅЕуЕФШ§НЧаЮгыЁїOCBЯрЫЦЃПШєДцдкЃЌЧыЧѓГіЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙњМвЛЗБЃОжЭГвЛЙцЖЈЃЌПеЦјжЪСПЗжЮЊ5МЖЃКЕБПеЦјЮлШОжИЪ§Дя0ЁЊ50ЪБЮЊ1МЖЃЌжЪСПЮЊгХЃЛ51ЁЊ100ЪБЮЊ2МЖЃЌжЪСПЮЊСМЃЛ101ЁЊ200ЪБЮЊ3МЖЃЌЧсЖШЮлШОЃЛ201ЁЊ300ЪБЮЊ4МЖЃЌжаЖШЮлШОЃЛ300вдЩЯЪБЮЊ5МЖЃЌжиЖШЮлШОЃЎФГГЧЪаЫцЛњГщШЁСЫ2015ФъФГаЉЬьЕФПеЦјжЪСПМьВтНсЙћЃЌВЂећРэЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыИљОнЭМжааХЯЂЃЌНтД№ЯТСаИїЬтЃК
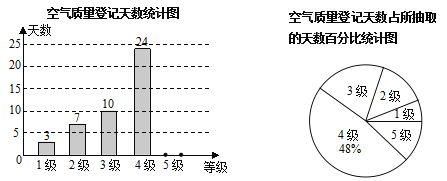
(1) БОДЮЕїВщЙВГщШЁСЫ ЬьЕФПеЦјжЪСПМьВтНсЙћНјааЭГМЦЃЛ
(2) ВЙШЋЬѕаЮЭГМЦЭМЃЛ
(3) ЩШаЮЭГМЦЭМжа3МЖПеЦјжЪСПЫљЖдгІЕФдВаФНЧЮЊ ЁуЃЛ
(4) ШчЙћПеЦјЮлШОДяЕНжаЖШЮлШОЛђепвдЩЯЃЌНЋВЛЪЪвЫНјааЛЇЭтЛюЖЏЃЌИљОнФПЧАЕФЭГМЦЃЌЧыФуЙРМЦ2015ФъИУГЧЪагаЖрЩйЬьВЛЪЪвЫПЊеЙЛЇЭтЛюЖЏЃЎ(2015ФъЙВ365Ьь)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮ![]() ЃЌЕу
ЃЌЕу![]() ЮЊЖдНЧЯп
ЮЊЖдНЧЯп![]() ЩЯвЛИіЖЏЕуЃЌ
ЩЯвЛИіЖЏЕуЃЌ![]() ЮЊ
ЮЊ![]() БпЩЯвЛЕуЃЌЧв
БпЩЯвЛЕуЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєЫФБпаЮ![]() ЕФУцЛ§ЮЊ25ЃЌЪдЬНЧѓ
ЕФУцЛ§ЮЊ25ЃЌЪдЬНЧѓ![]() гы
гы![]() ТњзуЕФЪ§СПЙиЯЕЪНЃЛ
ТњзуЕФЪ§СПЙиЯЕЪНЃЛ
ЃЈ3ЃЉШє![]() ЮЊЩфЯп
ЮЊЩфЯп![]() ЩЯЕФЕуЃЌЩш
ЩЯЕФЕуЃЌЩш![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЕФжмГЄЮЊ
ЕФжмГЄЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЎ
ЕФКЏЪ§ЙиЯЕЪНЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com