练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．要从电杆上离地面5m处向地面拉一长为13cm的电缆，则地面电缆固定处与电线杆底部的距离为（　　）
    A．10mB．11mC．12mD．13m

    分析 直接根据勾股定理进行解答即可．

    解答 解：如图，

    ∵电线杆、地面及缆绳正好构成直角三角形，AC=5m，BC=13m，
    ∴AB=$\sqrt{B{C}^{2}-A{C}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12（m）．
    故选：C．

    点评 本题考查的是勾股定理的应用，根据题意画出图形，熟练掌握勾股定理是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．下列运算错误的是（　　）
    A．（x2）3=x6B．x2•x3=x5C．x2-2xy+y2=（x-y）2D．3x-2x=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，将矩形纸片ABCD折叠，使点C与点A重合，折痕EF分别与AB、DC交于点E和点F．
    （1）证明：△ADF≌△AB′E；
    （2）若AD=12，DC=18，求△AEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

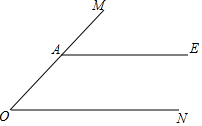    19．如图，A是∠MON边OM上一点，AE∥ON．
    （1）尺规作图，作∠MON的角平分线OB，交AE于点B；（保留作图痕迹，不写作法）
    （2）过点B画OB的垂线，分别交OM，ON于点C，D，求证：AB=$\frac{1}{2}$OC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，在?ABCD中，过点A作AE⊥BC、AF⊥DC，垂足分别为点E、F，AE、AF分别交BD于点G、H，且AG=AH．
    （1）求证：四边形ABCD是菱形；
    （2）延长AF、BC相交于点P，求证：BC2=DF•BP．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

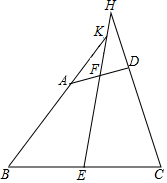    10．如图，在四边形ABCD中，AB=CD，E，F分别是BC，AD的中点，延长BA和CD分别与EF的延长线交于K，H．求证：∠BKE=∠CHE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，在△ABC中，点D，E分别是AC、AB上的中点，BD与CE相交于点O．求证：OC=2OE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

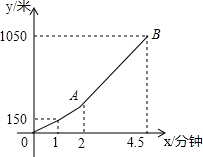    14．星期天的早晨，小明骑自行车从家出发，到离家1050米的书店买书，出发1分钟后，他到达离家150米的地方，又过1分钟后，小明加快了速度．如图所示是小明从家出发后离家的路程y（米）与他骑自行车的时间x（分钟）之间的函数图象．根据图象解答下列问题：
    （1）直接写出点A的坐标，并求线段AB所在的直线的函数解析式．
    （2）求小明出发多长时间后，离书店还剩210米的路程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．在△ABC中，AB=BC，∠B=90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．
    （1）如果点D在线段BC上运动，如图1：
    ①依题意补全图1；
    ②求证：∠BAD=∠EDC；
    ③通过观察、实验，小明得出结论：在点D运动的过程中，总有∠DCE=135°，．
    小明与同学讨论后，形成了证明这个结论的几种想法：
    想法一：在AB上取一点F，使得BF=BD，要证∠DCE=135°，只需证△ADF≌△DEC．
    想法二：以点D为圆心，DC为半径画弧交AC于点F，要证∠DCE=135°，只需证△AFD≌△DCE．
    想法三：过点E作BC所在直线的垂直线段EF，要证∠DCE=135°，只需证EF=CF．
    …
    请你参考上面的想法，证明∠DCE=135°
    （2）如果点D在线段CB的延长线上运动，利用图2画图分析，∠DCE的度数还是确定的值吗？如果是，直接写出∠DCE的度数；如果不是，说明理由．

    查看答案和解析>>

    同步练习册答案