练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．把抛物线y=x2-1先向右平移1个单位，再向上平移2个单位后得到的新抛物线的解析式为y=（x-1）2+1．

    分析 根据二次函数图象左加右减，上加下减的平移规律进行解答即可．

    解答 解：函数y=x2-1向右平移1个单位，得：y=（x-1）2-1；
    再向上平移2个单位，得：y=（x-1）2+1；
    故答案为：y=（x-1）2+1．

    点评 本题考查了二次函数的图象与几何变换，熟练掌握平移的规律：左加右减，上加下减是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．下列命题是真命题的是（　　）
    A．同位角相等
    B．有且只有一条直线与已知直线垂直
    C．垂线段最短
    D．直线外一点到这条直线的垂线段，叫做点到直线的距离

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，AD所在的直线是△ABC的对称轴，若BC=6，AD=5，则图中阴影部分的面积和为7.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．（1）计算：（-2）2+tan45°-（$\sqrt{3}$-2）0
    （2）化简：x（x+1）-（x+1）（x-2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．一个n边形过一个顶点有5条对角线，则n=8．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

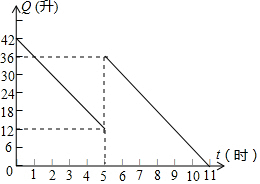    9．某机动车出发前油箱内有油42升，行驶若干小时后，途中在加油站加油若干升，油箱中余油量Q（升）与行驶时间t（时）之间的函数关系如图所示，回答下列问题．
      （1）机动车行驶几小时后加油？
      （2）求加油前油箱剩余油量Q与行驶时间t的函数关系，并求自变量t的取值范围；
      （3）中途加油多少升？
      （4）如果加油站距目的地还有230千米，车速为40千米/时，要到达目的地，油箱中的油是否够用？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．如图，在平面直角坐标系中，已知点A（-3，0），B（0，4），AB=5，对△AOB连续旋转变换，依次得到△1，△2，△3，△4…，则△2017的直角顶点的坐标为（　　）
    A．（4032，0）B．（4036，0）C．（8064，0）D．（8068，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

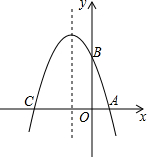    13．如图，在平面直角坐标系中，抛物线y=ax2+bx+3与x轴交于A、C两点，与y轴交于点B，且OA=1，OC=4．
    （1）求抛物线解析式；
    （2）在该抛物线上是否存在一点P，使得以点A、B、C、P为顶点的四边形为菱形？若存在，请求出P点坐标；若不存在，请说明理由；
    （3）已知点Q（5，3）和该抛物线上一动点M，试求当|QM-AM|的值最大时点M的坐标，并直接写出|QM-AM|的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

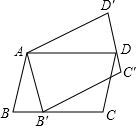    14．如图，?ABCD绕点A逆时针旋转45°，得到?AB′C′D′（点B′与B是对应点，点C′与点C是对应点，点D′与点D是对应点）．点B′恰好落在BC边上，则∠C=112.5°．

    查看答案和解析>>

    同步练习册答案