
【题目】如图,点D与点E分别是△ABC的边长BC、AC的中点,△ABC的面积是20cm![]() .
.

(1)求△ABD与△BEC的面积;
(2)△AOE与△BOD的面积相等吗?为什么?
【答案】(1)10,10;(2)相等,理由,见解析
【解析】
(1)要计算△ABE与△BCE的面积,可设点A到边BC的高为h,则S△ABD=![]() BD·h,S△ACD=
BD·h,S△ACD=![]() CD·h;再根据中点的定义得BD=CD,然后利用等量代换即可得到S△ABD=S△ACD,同理S△ABE=S△BCE,再结合△ABC的面积即可解决;
CD·h;再根据中点的定义得BD=CD,然后利用等量代换即可得到S△ABD=S△ACD,同理S△ABE=S△BCE,再结合△ABC的面积即可解决;
(2)结合上面的推理可得S△ABE=S△ABD,再根据图形可知S△ABE=S△ABO+S△AOE,S△ABD=S△ABO+S△BOD,
(1)可设点A到边BC的高为h,
则S△ABD=![]() BD·h,S△ACD=
BD·h,S△ACD=![]() CD·h,
CD·h,
∵点D是BC边的中点,
∴BD=CD.
∴S△ABD=S△ACD,
同理S△ABE=S△BCE,
∴S△ABD=S△BCE=![]() S△ABC=
S△ABC=![]() ×20=10(cm2).
×20=10(cm2).
(2)△AOE与△BOD的面积相等,理由如下.
根据(1)可得:S△ABE=S△ABD,
∵S△ABE=S△ABO+S△AOE,S△ABD=S△ABO+S△BOD,
∴S△AOE=S△BOD.


科目:初中数学 来源: 题型:
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有( )
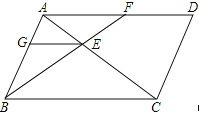
A.4对 B.5对 C.6对 D.7对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD,DE交BC于F,交AB的延长线于E,且∠EDB=∠C.
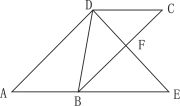
(1)求证:△ADE∽△DBE;
(2)若DE=9cm,AE=12cm,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,先把一矩形![]() 纸片上下对折,设折痕为
纸片上下对折,设折痕为![]() ;如图②,再把
;如图②,再把
点![]() 叠在折痕线
叠在折痕线![]() 上,得到
上,得到![]()
![]() .过
.过![]() 点作
点作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
(1)求证: ![]() ∽
∽![]() ;
;
(2)在图②中,如果沿直线![]() 再次折叠纸片,点
再次折叠纸片,点![]() 能否叠在直线
能否叠在直线![]() 上?请说明理由;
上?请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的长度.
的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若自然数![]() 使得三个数的加法运算“
使得三个数的加法运算“![]() ”产生进位现象,则称
”产生进位现象,则称![]() 为“连加进位数”.例如:2不是“连加进位数”,因为
为“连加进位数”.例如:2不是“连加进位数”,因为![]() 不产生进位现象;4是“连加进位数”,因为
不产生进位现象;4是“连加进位数”,因为![]() 产生进位现象;51是“连加进位数”,因为
产生进位现象;51是“连加进位数”,因为![]() 产生进位现象.如果从0,1,2,…,99这100个自然数中任取一个数,取到“连加进位数”的个数有( )个
产生进位现象.如果从0,1,2,…,99这100个自然数中任取一个数,取到“连加进位数”的个数有( )个
A.88B.89C.90D.91
查看答案和解析>>
科目:初中数学 来源: 题型:
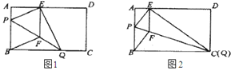
【题目】如图![]() ,在矩形纸片
,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() ,
,![]() 也随之移动.
也随之移动.
①当点![]() 与点
与点![]() 重合时(如图
重合时(如图![]() ),求菱形
),求菱形![]() 的边长;
的边长;
②若限定![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上移动,求出点
上移动,求出点![]() 在边
在边![]() 上移动的最大距离.
上移动的最大距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售每台进价分别为180元、150元的甲、乙两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
甲种型号 | 乙种型号 | ||
第一周 | 2台 | 3台 | 1100元 |
第二周 | 4台 | 5台 | 2000元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求甲、乙两种型号的电器的销售单价;
(2)若超市准备用不多于5000元的金额再采购这两种型号的电器共30台,求甲种型号的电器最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电器能否实现利润超过1900元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com