
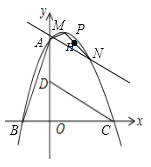
【题目】如图,在直角坐标系中有![]() ,
,![]() 为坐标原点,
为坐标原点,![]() ,将此三角形绕原点
,将此三角形绕原点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,二次函数
,二次函数![]() 的图象刚好经过
的图象刚好经过![]() 三点.
三点.
(1)求二次函数的解析式及顶点![]() 的坐标;
的坐标;
(2)过定点![]() 的直线
的直线![]() 与二次函数图象相交于
与二次函数图象相交于![]() 两点.
两点.
①若![]() ,求
,求![]() 的值;
的值;
②证明:无论![]() 为何值,
为何值,![]() 恒为直角三角形;
恒为直角三角形;
③当直线![]() 绕着定点
绕着定点![]() 旋转时,
旋转时,![]() 外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.
外接圆圆心在一条抛物线上运动,直接写出该抛物线的表达式.

【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②见解析;③
;②见解析;③![]() .
.
【解析】
(1)求出点A、B、C的坐标分别为(0,3)、(-1,0)、(3,0),即可求解;
(2)①S△PMN=![]() PQ×(x2-x1),则x2-x1=4,即可求解;②k1k2=
PQ×(x2-x1),则x2-x1=4,即可求解;②k1k2=![]() =-1,即可求解;③取MN的中点H,则点H是△PMN外接圆圆心,即可求解.
=-1,即可求解;③取MN的中点H,则点H是△PMN外接圆圆心,即可求解.
(1)![]() ,则
,则![]() ,
,
即点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 、
、![]() ,
,
则二次函数表达式为:![]() ,
,
即:![]() ,解得:
,解得:![]() ,
,
故函数表达式为:![]() ,
,
点![]() ;
;
(2)将二次函数与直线![]() 的表达式联立并整理得:
的表达式联立并整理得:
![]() ,
,
设点![]() 的坐标为
的坐标为![]() 、
、![]() ,
,
则![]() ,
,
则:![]() ,
,
同理:![]() ,
,
①![]() ,当
,当![]() 时,
时,![]() ,即点
,即点![]() ,
,
![]() ,则
,则![]() ,
,
![]() ,
,
解得:![]() ;
;
②点![]() 的坐标为
的坐标为![]() 、
、![]() 、点
、点![]() ,
,
则直线![]() 表达式中的
表达式中的![]() 值为:
值为:![]() ,直线
,直线![]() 表达式中的
表达式中的![]() 值为:
值为:![]() ,
,
为: ![]() ,
,
故![]() ,
,
即:![]() 恒为直角三角形;
恒为直角三角形;
③取![]() 的中点
的中点![]() ,则点
,则点![]() 是
是![]() 外接圆圆心,
外接圆圆心,
设点![]() 坐标为
坐标为![]() ,
,
则![]() ,
,
![]() ,
,
整理得:![]() ,
,
即:该抛物线的表达式为:![]() .
.


科目:初中数学 来源: 题型:
【题目】(本小题满分9分)如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.

(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 为正方形.点
为正方形.点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,一次函数
,一次函数![]() 的图象经过点
的图象经过点![]() 和点
和点![]() .
.
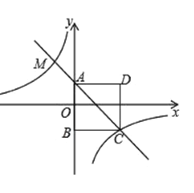
(1)求反比例函数与一次函数的解析式;
(2)写出![]() 的解集;
的解集;
(3)点![]() 是反比例函数图象上的一点,若
是反比例函数图象上的一点,若![]() 的面积恰好等于正方形
的面积恰好等于正方形![]() 的面积,求
的面积,求![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC切⊙O于点C,AB交⊙O于点D,BC的中点为 E,连接DE.
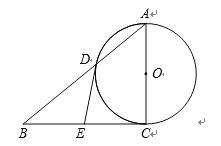
(1)求证:BE DE;
(2)连接EO交⊙O于点 F.填空:
①当∠B __________时,以 D,E,C,O为顶点的四边形是正方形;
②当∠B __________时,以 A,D,F,O为顶点的四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川资阳11分)在一个边长为a(单位:cm)的正方形ABCD中,点E、M分别是线段AC,CD上的动点,连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.
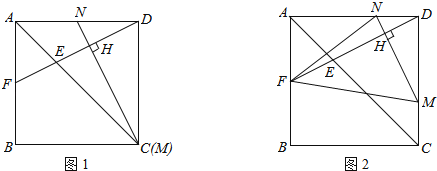
(1)如图1,当点M与点C重合,求证:DF=MN;
(2)如图2,假设点M从点C出发,以1cm/s的速度沿CD向点D运动,点E同时从点A出发,以![]() cm/s速度沿AC向点C运动,运动时间为t(t>0);
cm/s速度沿AC向点C运动,运动时间为t(t>0);
①判断命题“当点F是边AB中点时,则点M是边CD的三等分点”的真假,并说明理由.
②连结FM、FN,△MNF能否为等腰三角形?若能,请写出a,t之间的关系;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,一辆小汽车车门宽AO为1.2米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?______;(填“是”或“否”)请简述你的理由_______.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形![]() 中,
中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() (或它们的延长线)于点
(或它们的延长线)于点![]() .
.
当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),易证
时(如图1),易证![]() .
.
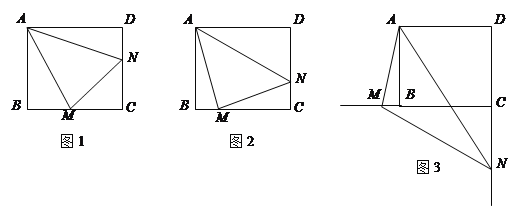
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图2),线段
时(如图2),线段![]() 和
和![]() 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.
(2)当![]() 绕点
绕点![]() 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段![]() 和
和![]() 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com