
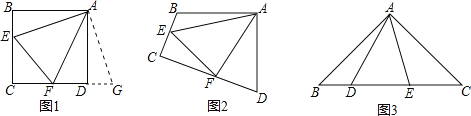
【题目】(1)探究:如图1和2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.
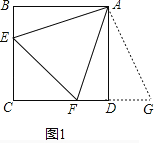
①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,则能证得EF=BE+DF,请写出推理过程;
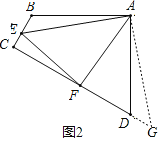
②如图2,若∠B、∠D都不是直角,则当∠B与∠D满足数量关系 时,仍有EF=BE+DF;
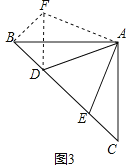
(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2![]() ,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.
,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.
【答案】(1)①理由详见解析;②∠B+∠ADC=180°;(2)![]() .
.
【解析】
试题分析:(1)①把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFG≌△AFE,根据全等三角形的性质得出EF=FG,即可得出答案;
②把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,证出△AFE≌△AFG,根据全等三角形的性质得出EF=FG,即可得出答案;
(2)把△ACE旋转到ABF的位置,连接DF,证明△AFE≌△AFG(SAS),则EF=FG,∠C=∠ABF=45°,△BDF是直角三角形,根据勾股定理得到BD2+CE2=DE2
,由∠BAC=90°,AB=AC=2![]() ,知BC=4,所以DC=3,EC=3﹣DE,代入解方程即可.
,知BC=4,所以DC=3,EC=3﹣DE,代入解方程即可.
试题解析:解:(1)①理由是:如图1,
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图1,
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线,
则∠DAG=∠BAE,AE=AG,
∠FAG=∠FAD+∠GAD=∠FAD+∠BAE=90°﹣45°=45°=∠EAF,
即∠EAF=∠FAG,
在△EAF和△GAF中,AF=AF,∠EAF=∠FAG,AE=AG,
∴△AFG≌△AFE(SAS),
∴EF=FG=BE+DF;
②当∠B+∠ADC=180°时,EF=BE+DF;
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图2,
∴∠BAE=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠EAF=∠FAG,
∵∠ADC+∠B=180°,
∴∠FDG=180°,点F、D、G共线,
在△AFE和△AFG中,AF=AF,∠EAF=∠FAG,AE=AG,
∴△AFE≌△AFG(SAS),
∴EF=FG,
即:EF=BE+DF,
故答案为:∠B+∠ADC=180°;
(2)把△ACE旋转到ABF的位置,连接DF,则∠FAB=∠CAE.
∵∠BAC=90°,∠DAE=45°,
∴∠BAD+∠CAE=45°,
又∵∠FAB=∠CAE,
∴∠FAD=∠DAE=45°,
则在△ADF和△ADE中,AD=AD,∠FAD=∠DAE,AF=AE,
∴△ADF≌△ADE,
∴DF=DE,∠C=∠ABF=45°,
∴∠BDF=90°,
∴△BDF是直角三角形
∴BD2+BF2=DF2,
∴BD2+CE2=DE2.
∵∠BAC=90°,AB=AC=2![]() ,
,
∴BC=4,
∵BD=1,
∴DC=3,EC=3﹣DE,
∴1+(3﹣DE)2=DE2,
解得:DE=![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1,Rt△BFC的面积为S2,Rt△DCE的面积为S3,则S1__ __S2+S3;(填“>”“=”或“<”)
(2)写出图中的三对相似三角形,并选择其中一对进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)如图,点E、F为线段BD的两个三等分点,四边形AECF是菱形.

(1)试判断四边形ABCD的形状,并加以证明;
(2)若菱形AECF的周长为20,BD为24,试求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.

(1)求证:四边形DEFG是平行四边形;
(2)若M为EF的中点,OM=3,∠OBC和∠OCB互余,求DG的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
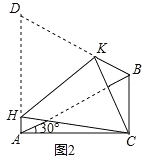
【题目】如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.
(1)求证:△AEF≌△BEC;
(2)判断四边形BCFD是何特殊四边形,并说出理由;
(3)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,若BC=1,求AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校召开运动会,七(1)班学生到超市分两次(第二次少于第一次)购买某种饮料90瓶,共用去205元,已知该种饮料价格如下:
购买瓶数/瓶 | 不超过30 | 30以上不超过50 | 50以上 |
单价/元 | 3 | 2.5 | 2 |
求:两次分别购买这种饮料多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)第一版=____%,“第四版”对应扇形的圆心角为________°;
(2)请你补全条形统计图;
(3)若该校有1200名学生,请你估计全校学生中最喜欢“第三版”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
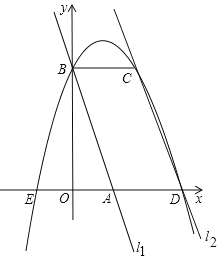
【题目】如图,在平面直角坐标系中两条直线为l1:y=–3x+3,l2:y=–3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中:
①a–b+c=0;
②2a+b+c=5;
③抛物线关于直线x=1对称;
④抛物线过点(b,c);
⑤S四边形ABCD=5;
其中正确的个数有( )
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com