
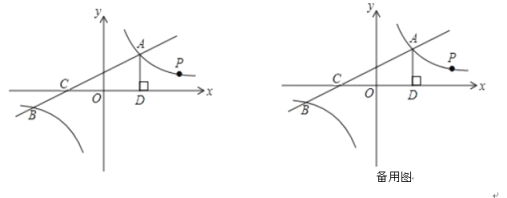
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹży1£½k1x+2Óė·“±ČĄżŗÆŹż![]() µÄĶ¼Ļó½»ÓŚµćA£Ø4£¬m£©ŗĶB£Ø©8£¬©2£©ÓėxÖį½»ÓŚµćC£®¹żµćA×÷AD”ĶxÖįÓŚµćD
µÄĶ¼Ļó½»ÓŚµćA£Ø4£¬m£©ŗĶB£Ø©8£¬©2£©ÓėxÖį½»ÓŚµćC£®¹żµćA×÷AD”ĶxÖįÓŚµćD
£Ø1£©ĒóŅ»“ĪŗÆŹżÓė·“±ČĄżŗÆŹżµÄ½āĪöŹ½£®
£Ø2£©øł¾ŻŗÆŹżĶ¼ĻóÖŖ£¬µ±y1£¾y2Ź±£¬xµÄȔֵ·¶Ī§ŹĒ £»
£Ø3£©Į¬½ÓBD£¬Ēó”÷ABDµÄĆ껿
£Ø4£©µćPŹĒ·“±ČĄżŗÆŹżŌŚµŚŅ»ĻóĻŽµÄĶ¼ĻóÉĻŅ»µć£¬ÉčÖ±ĻßOPÓėĻ߶ĪAD½»ÓŚµćE£¬µ±”÷ODE”×”÷CDAŹ±£¬ĒóµćPµÄ×ų±ź£®
”¾“š°ø”æ£Ø1£©![]() £»
£»![]() £»£Ø2£©
£»£Ø2£©![]() »ņ
»ņ![]() £»£Ø3£©24£»£Ø4£©
£»£Ø3£©24£»£Ø4£©![]()
”¾½āĪö”æ
£Ø1£©·Ö±š°ŃµćB“śČėŅ»“ĪŗÆŹżµÄ½āĪöŹ½ŗĶ·“±ČĄżŗÆŹżµÄ½āĪöŹ½£¬¼“æɵƵ½“š°ø£»
£Ø2£©½įŗĻµćA”¢BµÄŗį×ų±ź£¬Ņ»“ĪŗÆŹżĶ¼ĻńŌŚ·“±ČĄżŗÆŹżĶ¼ĻńµÄÉĻ·½£¬¼“æɵƵ½“š°ø£»
£Ø3£©×÷![]() ÓŚ
ÓŚ![]() £¬ĻČĒó³öµćAµÄ×ų±ź£¬Č»ŗóĒó³öADŗĶBEµÄ³¤¶Č£¬¼“æɵƵ½“š°ø£»
£¬ĻČĒó³öµćAµÄ×ų±ź£¬Č»ŗóĒó³öADŗĶBEµÄ³¤¶Č£¬¼“æɵƵ½“š°ø£»
£Ø4£©ÓÉĻąĖĘČż½ĒŠĪµÄŠŌÖŹ£¬µĆµ½![]() £¬Č»ŗóµĆµ½Ö±ĻßOPµÄ½āĪöŹ½£¬½įŗĻ·“±ČĄżŗÆŹżµÄ½āĪöŹ½£¬¼“æÉĒó³öµćPµÄ×ų±ź.
£¬Č»ŗóµĆµ½Ö±ĻßOPµÄ½āĪöŹ½£¬½įŗĻ·“±ČĄżŗÆŹżµÄ½āĪöŹ½£¬¼“æÉĒó³öµćPµÄ×ų±ź.
½ā£ŗ£Ø1£©½«µć![]() “śČė
“śČė![]() £¬Ōņ
£¬Ōņ
![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £»
£»
”ą![]()
½«µć![]() “śČė
“śČė![]() £¬Ōņ
£¬Ōņ
![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £®
£®
”ą![]() £»
£»
£Ø2£©”ßŅ»“ĪŗÆŹży1=k1x+2Óė·“±ČĄżŗÆŹż![]() µÄĶ¼Ļó½»ÓŚµćA£Ø4£¬m£©ŗĶB£Ø-8£¬-2£©£¬
µÄĶ¼Ļó½»ÓŚµćA£Ø4£¬m£©ŗĶB£Ø-8£¬-2£©£¬
”ąµ±y1£¾y2Ź±£¬xµÄȔֵ·¶Ī§ŹĒ£ŗ![]() »ņ
»ņ![]() £»
£»
¹Ź“š°øĪŖ£ŗ![]() »ņ
»ņ![]() £»
£»
£Ø3£©ČēĶ¼£ŗĮ¬½ÓBD£¬×÷![]() ÓŚ
ÓŚ![]() £¬
£¬

°Ńx=4“śČė![]() £¬µĆ
£¬µĆ![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬![]() £¬
£¬
”ß![]() £¬Ōņ
£¬Ōņ![]() £¬
£¬
”ą![]() £®
£®
£Ø4£©ČēĶ¼£ŗ
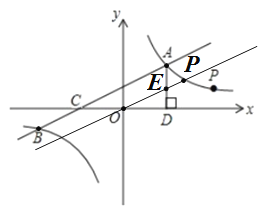
”ß![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ß![]() µÄ½āĪöŹ½ĪŖ£ŗ
µÄ½āĪöŹ½ĪŖ£ŗ![]() £¬
£¬
ÓÖ”ßÖ±ĻßOP¾¹żŌµćO£¬
”ąÖ±Ļß![]() µÄ½āĪöŹ½ĪŖ£ŗ
µÄ½āĪöŹ½ĪŖ£ŗ![]() £¬
£¬
ĮŖĮ¢Ö±Ļß![]() Óė·“±ČĄżŗÆŹż½āĪöŹ½×é³É·½³Ģ×飬
Óė·“±ČĄżŗÆŹż½āĪöŹ½×é³É·½³Ģ×飬
”ą £¬
£¬
½āµĆ£ŗ![]() £¬
£¬![]() £ØÉįČ„£©
£ØÉįČ„£©
”ą![]() £¬
£¬
”ą![]() .
.


 ĘߊĒĶ¼ŹéæŚĖćĖŁĖćĢģĢģĮ·ĻµĮŠ“š°ø
ĘߊĒĶ¼ŹéæŚĖćĖŁĖćĢģĢģĮ·ĻµĮŠ“š°ø ³õ֊ѧŅµæ¼ŹŌµ¼ÓėĮ·ĻµĮŠ“š°ø
³õ֊ѧŅµæ¼ŹŌµ¼ÓėĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĮŠ²ÄĮĻ£¬Ķź³É£Ø1£©~£Ø3£©Ģā£ŗ
ŹżŃ§æĪÉĻ£¬ĄĻŹ¦³öŹ¾ĮĖÕāŃłŅ»µĄĢā£ŗ
ČēĶ¼1£¬”÷ABCÖŠ£¬AB=AC£¬”ĻBAC=90”ć£¬µćDŹĒBCµÄÖŠµć£¬EŹĒACµÄÖŠµć£¬¾¹żµćA”¢C×÷ÉäĻßBEµÄ“¹Ļߣ¬“¹×ć·Ö±šĪŖµćF”¢G£¬Į¬½ÓAG£®Ģ½¾æĻ߶ĪDFŗĶAGµÄ¹ŲĻµ£®Ä³Ń§Ļ°Š”×éµÄĶ¬Ń§¾¹żĖ¼æ¼ŗ󣬽»Į÷ĮĖ×Ō¼ŗµÄĻė·Ø£ŗ
Š”Ć÷£ŗ”°¾¹ż¹Ū²ģŗĶ¶ČĮ棬·¢ĻÖ”ĻABFŗĶ”ĻACGĻąµČ£®”±Š”øÕ£ŗ”°¾¹ż¹Ū²ģŗĶ¶ČĮ棬·¢ĻÖÓŠĮ½ĢõĻ߶ĪŗĶAFĻąµČ£®”±
Š”Ī°£ŗ”°Ķعż¹¹ŌģČ«µČČż½ĒŠĪ£¬¾¹ż½ųŅ»²½ĶĘĄķ£¬æÉŅŌµĆµ½Ļ߶ĪDFŗĶAGµÄ¹ŲĻµ£®”±
””
ĄĻŹ¦£ŗ”°ČōµćE²»ŹĒACµÄÖŠµć£¬ĘäĖūĢõ¼ž²»±ä£ØČēĶ¼2£©£¬æÉŅŌĒó³ö![]() µÄÖµ£®”±
µÄÖµ£®”±
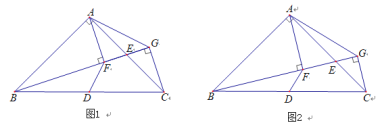
£Ø1£©ĒóÖ¤£ŗAF=FG£»
£Ø2£©Ģ½¾æĻ߶ĪDFŗĶAGµÄ¹ŲĻµ£¬²¢Ö¤Ć÷£»
£Ø3£©Ö±½ÓŠ“³ö![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĀ䏵”°ĆĄĄöĢ©ÖŻ”±µÄ¹¤×÷²æŹš£¬ŹŠÕžø®¼Ę»®¶Ō³ĒĒųµĄĀ·½ųŠŠøÄŌģ£¬ĻÖ°²Åżה¢ŅŅĮ½øö¹¤³Ģ¶ÓĶź³ÉøĆøÄŌģ¹¤×÷.ŅŃÖŖ¼×¶ÓµÄ¹¤×÷Š§ĀŹŹĒŅŅ¶Ó¹¤×÷Š§ĀŹµÄ![]() ±¶£¬¼×¶ÓøÄŌģ720Ć׵ĵĄĀ·±ČŅŅ¶ÓøÄŌģĶ¬Ńł³¤µÄµĄĀ·ÉŁÓĆ4Ģģ.
±¶£¬¼×¶ÓøÄŌģ720Ć׵ĵĄĀ·±ČŅŅ¶ÓøÄŌģĶ¬Ńł³¤µÄµĄĀ·ÉŁÓĆ4Ģģ.
(1)¼×”¢ŅŅĮ½¹¤³Ģ¶ÓĆæĢģÄÜøÄŌģµĄĀ·µÄ³¤¶Č·Ö±šŹĒ¶ąÉŁĆ×£æ
(2)Čō¼×¶Ó¹¤×÷Ņ»ĢģŠčø¶·ŃÓĆ7ĶņŌŖ£¬ŅŅ¶Ó¹¤×÷Ņ»ĢģŠčø¶·ŃÓĆ5ĶņŌŖ£¬ČōŠčøÄŌģµÄµĄĀ·Č«³¤2400Ć×£¬øÄŌģ×Ü·ŃÓĆ²»³¬¹ż195ĶņŌŖ£¬ŌņÖĮÉŁ°²Åż׶ӹ¤×÷¶ąÉŁĢģ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCµÄ±ßBCŌŚxÖįÉĻ£¬ĒŅ”ĻACB=90”ć£®·“±ČĄżŗÆŹży=![]() £Øx£¾0£©µÄĶ¼Ļó¾¹żAB±ßµÄÖŠµćD£¬ĒŅÓėAC±ßĻą½»ÓŚµćE£¬Į¬½ÓCD£®ŅŃÖŖBC=2OB£¬”÷BCDµÄĆ껿ĪŖ6£®
£Øx£¾0£©µÄĶ¼Ļó¾¹żAB±ßµÄÖŠµćD£¬ĒŅÓėAC±ßĻą½»ÓŚµćE£¬Į¬½ÓCD£®ŅŃÖŖBC=2OB£¬”÷BCDµÄĆ껿ĪŖ6£®
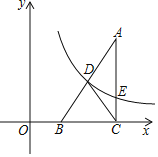
£Ø1£©ĒókµÄÖµ£»£Ø2£©ČōAE=BC£¬ĒóµćAµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ŹĒijŠ”×é×öÓĆʵĀŹ¹Ą¼ĘøÅĀŹ”°µÄŹµŃ鏱£¬»ę³öµÄijŅ»½į¹ū³öĻÖµÄʵĀŹÕŪĻßĶ¼£¬Ōņ·ūŗĻÕāŅ»½į¹ūµÄŹµŃéæÉÄÜŹĒ£Ø £©
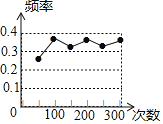
A. Å×Ņ»Ć¶Ó²±Ņ£¬³öĻÖÕżĆę³ÆÉĻ
B. “ÓŅ»øö×°ÓŠ2øöŗģĒņ1øöŗŚĒņµÄ“ü×ÓÖŠČĪČ”Ņ»Ēņ£¬Č”µ½µÄŹĒŗŚĒņ
C. Ņ»ø±Č„µō“óŠ”ĶõµÄĘĖæĖÅĘĻ“ŌČŗ󣬓ÓÖŠČĪ³éŅ»ÕÅÅʵĻØÉ«ŹĒŗģĢŅ
D. ÖĄŅ»Ć¶¾łŌȵÄÕżĮłĆęĢå÷»×Ó£¬³öĻÖ3µć³ÆÉĻ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
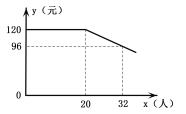
”¾ĢāÄæ”æĖę×ÅČĖĆĒÉś»īĖ®Ę½µÄĢįøߣ¬¶ĢĶ¾ĀĆŠŠČÕĒ÷»š±¬.ĪŅŹŠÄ³ĀĆŠŠÉēĶĘ³ö”°ĮÉŃō”ŖŗłĀ«µŗŗ£±õ¹Ū¹āŅ»ČÕÓĪ”±ĻīÄ棬ĶŶÓČĖ¾ł±ØĆū·ŃÓĆy£ØŌŖ£©ÓėĶŶӱØĆūČĖŹżx£ØČĖ£©Ö®¼äµÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£¬ĀĆŠŠÉē¹ę¶ØĶŶÓČĖ¾ł±ØĆū·ŃÓĆ²»ÄܵĶÓŚ88ŌŖ.ĀĆŠŠÉēŹÕµ½µÄĶŶÓ×ܱØĆū·ŃÓĆĪŖw£ØŌŖ£©.
£Ø1£©Ö±½ÓŠ“³öµ±x”Ż20Ź±£¬yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½¼°×Ō±äĮæxµÄȔֵ·¶Ī§£»
£Ø2£©¶łĶƽŚµ±ĢģĀĆŠŠÉēŹÕµ½Ä³øöĶŶӵÄ×ܱØĆū·ŃĪŖ3000ŌŖ£¬±ØĆūĀĆÓĪµÄČĖŹżŹĒ¶ąÉŁ£æ
£Ø3£©µ±Ņ»øöĶŶÓÓŠ¶ąÉŁČĖ±ØĆūŹ±£¬ĀĆŠŠÉēŹÕµ½µÄ×ܱØĆū·Ń×ī¶ą£æ×ī¶ą×ܱØĆū·ŃŹĒ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪ![]() ŹĒĮāŠĪ£¬
ŹĒĮāŠĪ£¬![]() ŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬
ŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£¬![]() .
.
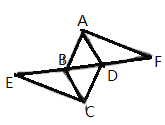
£Ø1£©ĒóÖ¤£ŗ![]() £»
£»
£Ø2£©µ±![]() Ź±£¬Ēó
Ź±£¬Ēó![]() µÄ¶ČŹż.
µÄ¶ČŹż.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬MNŹĒ”ŃOµÄÖ±¾¶£¬×÷AB”ĶMN£¬“¹×ćĪŖµćD£¬Į¬½ÓAM£¬AN£¬µćCĪŖ![]() ÉĻŅ»µć£¬ĒŅ
ÉĻŅ»µć£¬ĒŅ![]() £¬Į¬½ÓCM£¬½»ABÓŚµćE£¬½»ANÓŚµćF£¬ĻÖøų³öŅŌĻĀ½įĀŪ£ŗ¢ŁAD=BD£»¢Ś”ĻMAN=90”ć£»¢Ū
£¬Į¬½ÓCM£¬½»ABÓŚµćE£¬½»ANÓŚµćF£¬ĻÖøų³öŅŌĻĀ½įĀŪ£ŗ¢ŁAD=BD£»¢Ś”ĻMAN=90”ć£»¢Ū![]() £»¢Ü”ĻACM+”ĻANM=”ĻMOB£»¢ŻAE=
£»¢Ü”ĻACM+”ĻANM=”ĻMOB£»¢ŻAE=![]() MF£®
MF£®
ĘäÖŠÕżČ·½įĀŪµÄøöŹżŹĒ£Ø””””£©

A. 2 B. 3 C. 4 D. 5
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
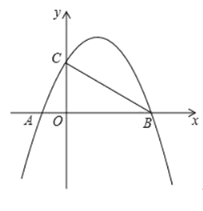
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßyax2bxc(a0)¾¹żA(1,0)£¬B(4,0)£¬C(0,2)Čżµć£®
£Ø1£©ĒóÕāĢõÅ×ĪļĻßŗĶÖ±ĻßBCµÄ½āĪöŹ½£»
£Ø2£©EĪŖÅ×ĪļĻßÉĻŅ»¶Æµć£¬ŹĒ·ń“ęŌŚµćE£¬Ź¹ŅŌA”¢B”¢EĪŖ¶„µćµÄČż½ĒŠĪÓėCOBĻąĖĘ£æČō“ęŌŚ£¬ŹŌĒó³öµćEµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com