
【题目】某中学为了解学生业余时间的活动情况,从看电视、看书、上网和运动四个方面进行了统计调查,随机调查了某班所有同学(每名同学必选且只能选一项最喜欢的活动),并将调查结果绘成了如下两个不完整的统计图,请根据图中信息回答下列问题:

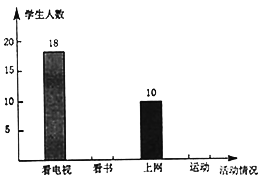
(1)被调查的班级学生共有______名:
(2)补全条形统计图;
(3)扇形统计图中“上网”的学生所对应的圆心角是_____度:
(4)该校一共有1200名学生,根据抽样调查结果,请你计算出该校大约有多少名学生喜欢“运动”?
【答案】(1)50;(2)补图见解析;(3)72;(4)192名
【解析】
(1)用喜欢看电视的人数除以它所占百分比即可得答案;(2)用总人数乘以喜欢看书的学生所占百分比可得喜欢看书的学生人数,总人数减去喜欢看电视、看书、上网的学生人数可得喜欢运动的学生人数,补全条形统计图即可;(3)用360°乘以喜欢上网的学生所占百分比即可得答案;(4)用1200乘以喜欢运动的学生所占百分比即可得答案.
(1)18÷36%=50(名)
∴被调查的班级学生共有50名
故答案为:50
(2)喜欢看书的人数为:50×28%=14(名),
喜欢运动的人数为:50-18-14-10=8(名),
补全条形统计图如下:
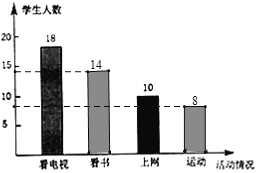
(3)“上网”的学生所对应的圆心角是:360°×![]() =72°,
=72°,
故答案为:72
(4)1200×![]() =192(名),
=192(名),
答:该校大约有192名学生喜欢“运动”.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,认真观察下面这些算式,并结合你发现的规律,完成下列问题:

(1)请写出:
算式⑤ ;
算式⑥ ;
(2)上述算式的规律可以用文字概括为:“两个连续奇数的平方差能被8整除”,如果设两个连续奇数分别为![]() 和
和![]() (
(![]() 为整数),请说明这个规律是成立的;
为整数),请说明这个规律是成立的;
(3)你认为“两个连续偶数的平方差能被8整除”这个说法是否也成立呢?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程![]() ,
,![]() ,其中
,其中![]() ,下列四个结论中,错误的是( )
,下列四个结论中,错误的是( )
A. 如果方程![]() 有两个不相等的实数根,那么方程
有两个不相等的实数根,那么方程![]() 也有两个不相等的实数根
也有两个不相等的实数根
B. ![]() 时,方程
时,方程![]() 和方程
和方程![]() 有一个相同的根,那么这个根必是
有一个相同的根,那么这个根必是![]()
C. 如果![]() 是方程
是方程![]() 的一个根,那么
的一个根,那么![]() 是方程
是方程![]() 的一个根
的一个根
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),弧AA1是以点B为圆心,BA为半径的圆弧;弧A1A2是以点O为圆心,OA1为半径的圆弧;弧A2A3是以点C为圆心,CA2为半径的圆弧;弧A3A4是以点A为圆心,AA3为半径的圆弧,继续以点B,O,C,A为圆心按上述作法得到的曲线AA1A2A3A4A5…称为正方形的“渐开线”,则点 A4的坐标是____,那么 A4n+1的坐标为____.
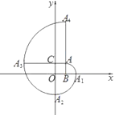
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过![]() 轴正半轴上的任意一点
轴正半轴上的任意一点![]() ,作
,作![]() 轴的平行线,分别与反比例函数
轴的平行线,分别与反比例函数![]() 和
和![]() 的图象交于点
的图象交于点![]() 和点
和点![]() ,点
,点![]() 是
是![]() 轴上一点,连接
轴上一点,连接![]() 、
、![]() ,则
,则![]() 的面积为( )
的面积为( )

A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过点B(﹣2,0)的直线y=kx+b与直线y=4x+2相交于点A(﹣1,﹣2),4x+2<kx+b<0的解集为( )
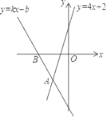
A.x<﹣2B.﹣2<x<﹣1C.x<﹣1D.x>﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
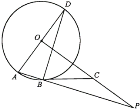
【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.
(1)求证:∠CBP=∠ADB.
(2)若OA=2,AB=1,求线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.
(1)求证:△ADE∽△BEC.
(2)若AD=1,BC=3,AE=2,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动{即(0,0)﹣(0,1)﹣(1,1)﹣(1,0)…},且每秒移动一个单位,那么第35秒时质点所在位置的坐标是( )
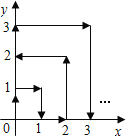
A. (4,0)B. (5,0)C. (0,5)D. (5,5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com