
【题目】(1)(问题发现)
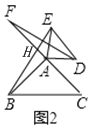
如图1,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,延长CA到点F,使得AF=AC,连接DF、BE,则线段BE与DF的数量关系为 ,位置关系为 ;
(2)(拓展研究)
将△ADE绕点A旋转,(1)中的结论有无变化?仅就图(2)的情形给出证明;
(3)(解决问题)
当AB=2,AD=![]() ,△ADE旋转得到D,E,F三点共线时,直接写出线段DF的长.
,△ADE旋转得到D,E,F三点共线时,直接写出线段DF的长.

【答案】(1)DF=BE,DF⊥BE;(2)详见解析;(3)DF=![]() +1或
+1或![]() ﹣1
﹣1
【解析】
(1)通过证明△ABE≌△AFD,可得DF=BE,DF⊥BE;
(2)通过证明△ADF≌△AEB,可得DF=BE,DF⊥BE;
(3)分点D在AB左侧和右侧两种情况讨论,由等腰直角三角形的性质和勾股定理可求FH的长,即可求DF的长.
(1)延长FD交BE于点M

∵△ABC和△ADE都是等腰直角三角形
∴AD=AE,AB=AC,∠BAC=90°=∠FAD
∵AF=AC
∴AF=AB,且AD=AE,∠BAE=∠DAF=90°
∴△ABE≌△AFD(SAS)
∴FD=BE,∠F=∠ABE,
∵∠ABE+∠AEB=90°
∴∠F+∠AEB=90°
∴∠FME=90°
∴FD⊥BE
故答案为:DF=BE,DF⊥BE
【拓展研究】
(2)
∵∠BAC=90°=∠EAD
∴∠DAF=∠EAB=90°+∠EAF
在△ADF 和△AEB 中
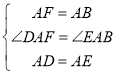
∴△ADF≌△AEB
DF=BE,∠F=∠EBA
设 CF 和 BE 相交于点 H,则∠EHF=∠CHB
∵∠BAC=∠DAE=90°
∴∠EBA+∠CHB=90°
∴∠F+∠EHF=90°
∴DF⊥BE
(3)当点D在AB的左侧,
如图,过点A作AH⊥EF于点H,

∵△ADE是等腰直角三角形,AD=AE=![]() ,AH⊥EF
,AH⊥EF
∴DE=2,AH=DH=![]() DE=1
DE=1
∵FH=![]() =
=![]()
∴FD=FH﹣DH=![]() ﹣1
﹣1
当点D在AB右侧,
如图,过点A作AH⊥EF于点H,
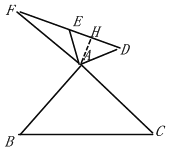
同理可求:FH=![]()
∴FD=FH+HD=![]() +1
+1
综上所述:DF=![]() +1或
+1或![]() ﹣1
﹣1


科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
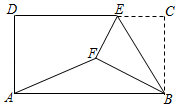
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接AE、DE.

(1)求证:DE是⊙O的切线;
(2)设△CDE的面积为 S1,四边形ABED的面积为 S2.若 S2=5S1,求tan∠BAC的值;
(3)在(2)的条件下,若AE=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕AO与边BC交于点O,连结AP、OP.
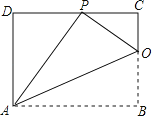
(1)求证:△PDA∽△OCP;
(2)若tan∠PAO=![]() ,求CP的长.
,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的
,求一个一元二次方程,使它的根分别是已知方程根的![]() 倍
倍
解:设所求方程的根为![]() ,则
,则![]() ,所以
,所以![]() .
.
把![]() 代入已知方程,得
代入已知方程,得![]() .
.
化简,得![]()
故所求方程为![]() .
.
这种利用方程的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式).
(1)已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为:_______________.
,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为:_______________.
(2)已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的倒数.
,求一个一元二次方程,使它的根分别是已知方程根的倒数.
(3)已知关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() )的两个实数根分别为
)的两个实数根分别为![]() ,
,![]() ,求一元二次方程
,求一元二次方程![]() 的两根.(直接写出结果)
的两根.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1,M2,M3,…Mn分别为边B1B2,B2B3,B3B4,…,BnBn+1的中点,△B1C1M1的面积为S1,△B2C2M2的面积为S2,…△BnCnMn的面积为Sn,则Sn= .(用含n的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数y=-x2+bx+c的图像与x轴的交点为点A(3,0)和点B,与y轴交于点C(0,3),连接AC.
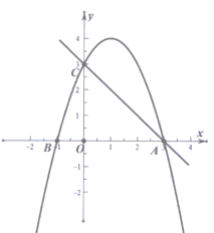
(1)求这个二次函数的解析式;
(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△ACD的面积最大?若存在,求出点D的坐标及△ACD面积的最大值,若不存在,请说明理由.
(3)在抛物线上是否存在点E,使得△ACE是以AC为直角边的直角三角形如果存在,请直接写出点E的坐标即可;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com