
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
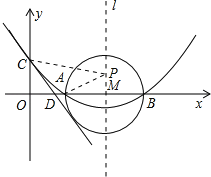
(1)求抛物线的解析式及A,B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)在以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
【答案】解:(1)由题意,设抛物线的解析式为![]() (a≠0)
(a≠0)
∵抛物线经过(0,2)∴![]() ,解得:
,解得:![]() 。
。
∴抛物线的解析式为![]() ,即:
,即:![]() 。
。
令y=0时,![]() ,解得:x=2或x=6。
,解得:x=2或x=6。
∴A(2,0),B(6,0)。
(2)存在。
如图1,由(1)知:抛物线的对称轴l为x=4,
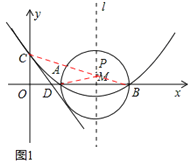
因为A、B两点关于l对称,连接CB交l于点P,则AP=BP,所以AP+CP=BC的值最小。
∵B(6,0),C(0,2),∴OB=6,OC=2。∴BC=2![]() 。
。
∴AP+CP=BC=2![]() 。
。
∴AP+CP的最小值为2![]() 。
。
(3)如图2,连接ME,
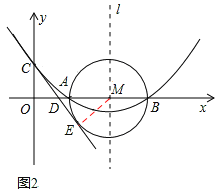
∵CE是⊙M的切线,∴ME⊥CE,∠CEM=90°。
由题意,得OC=ME=2,∠ODC=∠MDE,
∵在△COD与△MED中,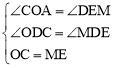 ,
,
∴△COD≌△MED(AAS)。∴OD=DE,DC=DM。
设OD=x,则CD=DM=OM﹣OD=4﹣x,
∵在Rt△COD中,OD2+OC2=CD2,∴![]() ,解得x=
,解得x=![]() 。
。
∴D(![]() ,0)。
,0)。
设直线CE的解析式为y=kx+b,
∵直线CE过C(0,2),D(![]() ,0)两点,
,0)两点,
则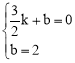 ,解得:
,解得: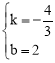 。
。
∴直线CE的解析式为![]() 。
。
【解析】
试题(1)利用顶点式求得二次函数的解析式后令其等于0后求得x的值即为与x轴交点坐标的横坐标。
(2)根据轴对称的性质,线段BC的长即为AP+CP的最小值。
(3)连接ME,根据CE是⊙M的切线得到ME⊥CE,∠CEM=90°,从而证得△COD≌△MED,设OD=x,在Rt△COD中,利用勾股定理求得x的值即可求得点D的坐标,然后利用待定系数法确定线段CE的解析式即可。


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
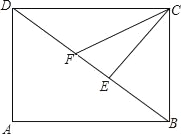
【题目】如图,矩形ABCD中,CE⊥BD于E,CF平分∠DCE与DB交于点F.
(1)求证:BF=BC;
(2)若AB=4cm,AD=3cm,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
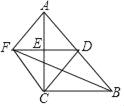
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别是边AB、AC的中点,延长DE至F,使得AF∥CD,连接BF、CF.
(1)求证:四边形AFCD是菱形;
(2)当AC=4,BC=3时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
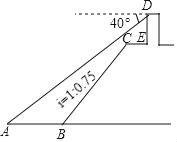
【题目】如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为多少米?(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表.
对雾霾了解程度的统计表:
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
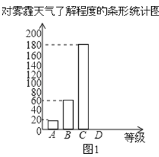
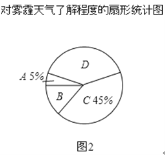
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6个型号):
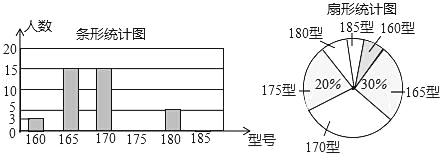
根据以上信息,解答下列问题:
(1)该班共有 名学生;
(2)补全条形统计图;
(3)该班学生所穿校服型号的众数为 ,中位数为 ;
(4)如果该校预计招收新生1500名,根据样本数据,估计新生穿170型校服的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为﹣3和1;④a﹣2b+c>0,其中正确的命题是( )
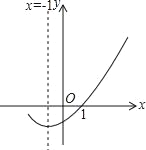
A. ①②③B. ①③C. ①④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径为13的⊙E,经过原点O,并且与x轴、y轴分别交于A、B两点,线段OA、OB(OA>OB)的长分别是方程x2+kx+60=0的两根.
(1)OA:OB=____;
(2)若点C在劣弧OA上,连结BC交OA于D,当△BOC∽△BDA时,点D的坐标为______.
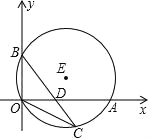
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,![]() ,点E在边CD上,且
,点E在边CD上,且![]() ,
,![]() 与
与![]() 关于AE所在的直线成对称图形
关于AE所在的直线成对称图形![]() 以点A为中心,把
以点A为中心,把![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,连接GF,则线段GF的长为______.
,连接GF,则线段GF的长为______.
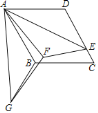
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com