
分析 (1)把x=a代入方程求出a2-4a=-1,再代入求出即可;
(2)解方程求出a的值,再根据二次根式的性质和分式的运算法则进行化简,最后代入求出即可.
解答 解:(1)∵a是一元二次方程x2-4x+1=0的根,
∴a2-4a+1=0,
∴a2-4a=-1;
∴a2-4a+2015=-1+2015=2014;
(2)原方程的解是:x=$\frac{4±2\sqrt{3}}{2}$=2±$\sqrt{3}$,
∵a是一元二次方程x2-4x+1=0的两个实数根中较小的根,
∴a=2-$\sqrt{3}$,且a-1<0,
∴$\frac{1-2a+a2}{a-1}$-$\frac{\sqrt{a2-2a+1}}{a2-a}$-$\frac{1}{a}$
=$\frac{(a-1)2}{a-1}$-$\frac{|a-1|}{a(a-1)}$-$\frac{1}{a}$
=a-1-$\frac{-(a-1)}{a(a-1)}$-$\frac{1}{a}$
=a-1+$\frac{1}{a}$-$\frac{1}{a}$
=a-1,
当a=2-$\sqrt{3}$时,原式=2-$\sqrt{3}$-1=1-$\sqrt{3}$.
点评 本题考查了解一元二次方程,二次根式的性质,分式的混合运算的应用,能正确运用法则进行化简是解此题的关键,难度适中.


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 4和16 | C. | 1或3 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,铁路上A,B两站(视为直线上两点)相距14km,C,D为两村庄(可看为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现要在铁路上建一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站多少km处?
如图所示,铁路上A,B两站(视为直线上两点)相距14km,C,D为两村庄(可看为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现要在铁路上建一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站多少km处?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 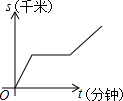 | C. | 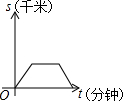 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com