
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬��y�ύ�ڵ�C����OA=2��OC=3��
��x�ύ��A��B���㣬��y�ύ�ڵ�C����OA=2��OC=3��

��1���������ߵĽ���ʽ��
��2����Rt��OBC�ĸ�OD���ӳ�OD���������ڵ�һ�����ڽ��ڵ�E�����E�����ꣻ
��3������x���Ϸ����������ϣ��Ƿ����һ��P��ʹ�ı���OBEP��ƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���������ߵĶԳ����ϣ��Ƿ�����ϵ�Q��ʹ����BEQ���ܳ���С�������ڣ������Q�����ꣻ�������ڣ���˵��������
���𰸡���1�������߽���ʽΪy=-![]() x2+
x2+![]() x+3����2����E��������2��2����
x+3����2����E��������2��2����
��������
�����������1���ȸ�����֪�����ó�A�㼰C�����꣬���ô���ϵ������������������ߵĽ���ʽ��
��2��y=0���루1����������κ����Ľ���ʽ���ɵij��˺�����x��Ľ������꣬��ODƽ����BOC��֪OE���ڵ�ֱ��Ϊy=x���ٽ��ֱ������������ɵķ����鼴�����E�����ꣻ
��3��������E��x���ƽ�����������߽�����һ��P������BE��PO����y=2������κ�������ʽ�������P�����꣬�����ɵó��ı���OBEP��ƽ���ı��Σ�
����Q�������߶Գ����ϵ�һ�㣬����QA��QB��QE��BE����QA=QB��֪��BEQ���ܳ�����BE+QA+QE����A��E���������ɵó�ֱ��AE�Ľ���ʽ���ٸ��������ߵĶԳ�����x=![]() �����Q������꣬�����ɵó�������
�����Q������꣬�����ɵó�������
����������⣺��1����OA=2��
����A��������-2��0����
��OC=3��
����C��������0��3����
���ѣ�-2��0������0��3������y=-![]() x2+bx+c����
x2+bx+c����![]()
���![]()
�������߽���ʽΪy=-![]() x2+
x2+![]() x+3��
x+3��
��2����y=0����y=-![]() x2+
x2+![]() x+3��
x+3��
���x1=-2��x2=3
����B��������3��0����
��OB=OC=3
��OD��BC��
��ODƽ����BOC
��OE���ڵ�ֱ��Ϊy=x
�ⷽ���� ��
�� ��
�� ��
��
����E�ڵ�һ�����ڣ�
����E��������2��2����
��3�������ڣ���ͼ1������E��x���ƽ�����������߽�����һ��P������BE��PO��

��y=2����y=-![]() x2+
x2+![]() x+3��
x+3��
���x1=-1��x2=2
����P��������-1��2����
��PE��OB����PE=OB=3��
���ı���OBEP��ƽ���ı��Σ�
����x���Ϸ����������ϣ�����һ��P��-1��2����ʹ���ı���OBEP��ƽ���ı��Σ�
�����ڣ���ͼ2����Q�������߶Գ����ϵ�һ�㣬����QA��QB��QE��BE��

��QA=QB��
���BEQ���ܳ�����BE+QA+QE��
����BE�ij��Ƕ�ֵ��
��A��Q��E��ͬһֱ����ʱ����BEQ���ܳ���С��
��A��-2��0����E��2��2���ɵ�ֱ��AE�Ľ���ʽΪy=![]() x+1��
x+1��
�������ߵĶԳ�����x=![]()
����Q��������![]() ��
��![]() ��
��
���������ߵĶԳ����ϣ����ڵ�Q��![]() ��
��![]() ����ʹ����BEQ���ܳ���С��
����ʹ����BEQ���ܳ���С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
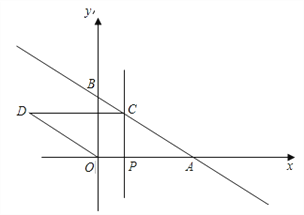
����Ŀ����ͼ����ֱ֪��y=kx+b��x�ύ��A��8��0������y�ύ��B��0��6������P��x���������ϵ�һ���㣬����P��PC��x�ᣬ��ֱ��AB�ڵ�C����OA��ACΪ�߹�����OACD�����P�ĺ�����Ϊm��
��1����ֱ��AB�ĺ�������ʽ��
��2�����ı���OACDǡ�����Σ������m��ֵ��
��3���ڣ�2���������£�y������Ƿ���ڵ�Q������CQ��ʹ�á�OQC+��ODC=180�㣮�����ڣ�ֱ��д�����з��������ĵ�Q�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ����̽����������������1��3��5��7�����г���ͼ��������ʮ�ֿ���5��������ͼ�� 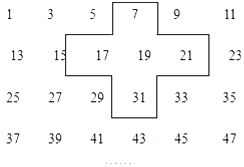
��1������ʮ�ֿ���������ƽ�ƣ���һ��Ҫ��ס�����е�5�����������м����Ϊa����a�Ĵ���ʽ��ʾʮ�ֿ��ס��5������֮�ͣ�
��2��ʮ�ֿ��ס��5����֮���ܵ���2015�����ܣ��ֱ�д��ʮ�ֿ��ס��5�����������ܣ���˵�����ɣ�
��3��ʮ�ֿ��ס��5����֮���ܵ���365�����ܣ��ֱ�д��ʮ�ֿ��ס��5�����������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P�ǡ�O��һ�㣬PA�С�O�ڵ�A��AB�ǡ�O��ֱ��������OP������B��BC��OP����O�ڵ�C������AC��OP�ڵ�D��
��1����֤��PC�ǡ�O�����ߣ�
��2����PD=![]() cm��AC=8cm����ͼ����Ӱ���ֵ������
cm��AC=8cm����ͼ����Ӱ���ֵ������
��3���ڣ�2���������£�����E�ǻ�AB���е㣬����CE����CE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=kx��
��1��������ͼ���ڶ��������ޣ���k�ķ�Χ��ʲô��
��2���㣨1��-2��������ͼ���ϣ������ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACE���ԡ�ABCD�ĶԽ���ACΪ�ߵĵȱ������Σ���C���E����x��Գ�.��E��������ǣ�7����3 ![]() ������D��������� ( )
������D��������� ( )
A.(4,0)
B.( ![]() ,0)
,0)
C.(5,0)
D.( ![]() ,0)
,0)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD��ƽ���ı��Σ����н����в���ȷ���ǣ� �� 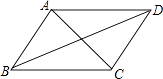
A.��AB=BCʱ����������
B.��AC��BDʱ����������
C.����ABC=90��ʱ�����Ǿ���
D.��AC=BDʱ������������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com