练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    M是正方形ABCD内一点，∠MAC=∠MCD=19°，则∠AMC=
     
    ．
    考点：正方形的性质
    专题：计算题
    分析：AC为正方形的对角线，故AC为角平分线，已知∠MAC=∠MCD=19°，可以证明∠MAC+∠MCA=45°，在△ACM中，根据三角形内角和为180°，可以求∠AMC的大小．
    解答：解：由题意知：∠MAC=∠MCD=19°
    ∵正方形中对角线即角平分线，
    故∠ACM=45°-∠MCD，
    ∴∠ACM+∠CAM=45°-∠MCD+∠MAC=45°，
    ∴∠AMC=180°-45°=135°，
    故答案为135°．
    点评：本题考查了正方形对角线即角平分线的性质，考查了三角形内角和为180°的性质，本题中求∠ACM+∠CAM=45°是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    将等腰三角形纸片ABC的底边BC折起，使点C落在腰上，这时纸片的不重合部分也是等腰三角形，则∠A=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    矩形ABCD的对角线AC=5，已知矩形的长AB=4，则矩形ABCD的面积是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

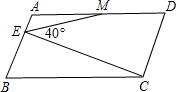    （Figure 1）In the parallelogram ABCD，AD=2AB，a point M is mid-point of segment AD，CE⊥AB，if∠CEM=40°，then the value of∠DME is（　　）
    A、150°B、140°
    C、135°D、130°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，ABCG和CDEF分别是边长为10cm、12cm的正方形，则图中阴影部分的面积是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知方程x2+ax-b=0的根是a和c，方程x2+cx+d=0的根是b和d．其中，a、b、c、d为不同实数，求a、b、c、d的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知
    x2
    x2-2
    =
    1
    1-
    		3
    -
    		2
    ，那么(
    1
    1-x
    -
    1
    1+x
    )÷(
    x
    x2-1
    +x)    =
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

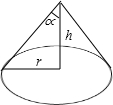    飞行员在空中寻找成功返回地面的载入飞船“神州五号”，观察范围是一个圆，如图，设飞机的高度h=480米，观测角α=45°，他看到的地面面积是
     
    平方米．如果观测角不变，要使看到的地面面积增加到原来的2倍，飞机要升高
     
    米（π取3.14，结果精确到0.1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：
    (x-y)(z-x)
    (x-2y+z)(x+y-2z)
    +
    (z-y)(x-y)
    (x+y-2z)(y+z-2x)
    +
    (x-z)(y-z)
    (y+z-2x)(x-2y+z)
    ．

    查看答案和解析>>

    同步练习册答案