练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．为了加强公民的节水意识，合理利用水资源，某城市规定用水收费标准如下：每户每月用水量不超过6m3，水费按按0.6元/m3；每户每月用水量超过6m3时，超过的部分按1元/m3收费．设每户每月用水量为xm3，应缴费为y元．
    （1）写出每月用水量不超过6m3和超过6m3时，y与x之间函数关系式，并判断它们是否为一次函数；
    （2）已知某户5月份的用水量为8m3，求该户5月份应交的水费．

    分析 （1）分别根据每月用水不超过6m3和超过6m3时的收费标准，即可得出y与x的函数关系式；
    （2）将x=8，代入函数关系式即可得出答案．

    解答 解：（1）当0≤x≤6时，y=0.6x；当x＞6时，y=6×0.6+（x-6）=x-2.4；都是一次函数；
    （2）把x=8代入y=x-2.4中，得：y=8-2.4=5.6元．
    答：该用户5月份的水费是5.6元．

    点评 本题考查了函数关系式，解答本题的关键是根据收费标准列出函数关系式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．2013年8月由于持续高温和长时间无雨，南湖蓄水库的水量随着时间的增加而减少，干旱持续时间t天与蓄水量v（万立方米）的关系如图所示，回答下列问题：
    （1）干旱持续10天，蓄水量为多少？
    （2）蓄水量小于400万立方米时将发出严重干旱警报，那么干旱多少天后将会发出严重干旱警报？
    （3）按照这个规律，预计持续干旱多少天水库将干涸？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．如图，在Rt△ABC中，∠ABC=90°，AB=3，AC=5，点E在BC上，将△ABC沿AE折叠，使点B落在AC边上的点B′处，则BE的长为（　　）
    A．1B．1.5C．2D．2.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．如图，A点在半径为2的⊙O上，过线段OA上的一点P作直线m，与⊙O过A点的切线交于点B，且∠APB=60°，设OP=x，则△PAB的面积y关于x的函数图象大致是（　　）
    A．B．C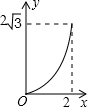．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．甲乙两名运动员进行长跑训练，两人距终点的路程y（米）与跑步时间x（分）之间的函数的图象如图所示，根据图象所提供的信息解答下列问题：
    （1）他们进行5000米的长跑训练，在0＜x＜15的时间段内，速度较快的人是甲；
    （2）求甲距终点的路程y（米）和跑步时间x（分）之间的函数关系式；
    （3）当x=15时，两人相距多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．画图：已知线段a、b．
    （1）画△ABC，使AB=a，BC=b，∠B=45°；
    （2）画出（1）中△ABC的角平分线AD；
    （3）过点D作DE⊥AB，垂足为点E，如果点D到直线AB的垂线段的长度为1.7，那么点D到直线AC的距离为1.7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图所示，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，如图①，将△ADE绕A点顺时针旋转一定角度，得到图②；然后将BD、CE分别延长至M、N，使DM=$\frac{1}{2}$BD，EN=$\frac{1}{2}$CE，得到图③；若AB=k•AC（k＞1），按上述操作方法，得到图④．下列结论：
    （1）在图②中，若AB=AC，则BD=CE  
    （2）在图③中，若AB=AC，则AM=AN  
    （3）在图③中，若AB=AC，则∠MAN=∠BAC  
    （4）在图④中，AM=kAN、∠MAN=∠BAC 
    （5）在图④中，△ADE∽△AMN．
    其中正确的有（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，一个机器人从O点出发，向正东方向走3m，到达A1点，再向正北走6m到达A2点，再向正西走9m到达A3点，再向正南走12m，到达A4点，再向正东方向走15m到达A5点，按如此规律走下去，当机器人走到A6点时，A6点的坐标是（　　）
    A．（9，12）B．（9，9）C．（9，6）D．（9，3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．若关于x的分式方程$\frac{2m+x}{x-3}$-1=$\frac{2}{x}$无解，则m的值为（　　）
    A．-l．5B．1C．-l．5或2D．-0.5或-l．5

    查看答案和解析>>

    同步练习册答案