
【题目】如图,点A,B,C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
(1)求证:AP是⊙O的切线;
(2)求PD的长.
【答案】
(1)解:证明:连接OA.

∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠ACP=∠CAO=30°,
∴∠AOP=60°,
∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=90°,
∴OA⊥AP,
∴AP是⊙O的切线,
(2)解:连接AD.
∵CD是⊙O的直径,
∴∠CAD=90°,
∴AD=ACtan30°=3× ![]() =
= ![]() ,
,
∵∠ADC=∠B=60°,
∴∠PAD=∠ADC﹣∠P=60°﹣30°=30°,
∴∠P=∠PAD,
∴PD=AD= ![]() .
.
【解析】(1)连接OA,由直径所对的圆周角为90°可得到∠DAC=90°,故此可得到∠ACP=∠APC=30°,然后再求得∠AOP=60°,从而得到∠PAO=90°;(2)由直径所对的圆周角为90°可得到∠DAC=90°,然后利用三角函数与等腰三角形的判定定理可求得PD的长.
【考点精析】利用圆周角定理和切线的判定定理对题目进行判断即可得到答案,需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


科目:初中数学 来源: 题型:
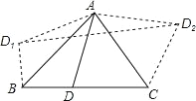
【题目】如图,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2![]() +2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
+2,D是BC边上异于点B,C的一动点,将三角形ABD沿AB翻折得到△ABD1,将△ACD沿AC翻折得到△ACD2,连接D1D2,则四边形D1BCD2的面积的最大值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)当![]() 时,直接写出
时,直接写出![]() 的取值范围
的取值范围

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )

A. (2,5)B. (5,2)C. (2,﹣5)D. (5,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图: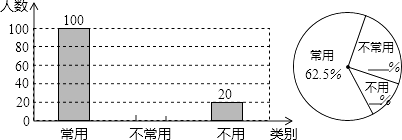
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x2+(a+3)x+a+1=0是关于x的一元二次方程.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1 , x2 , 且x12+x22=10,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在AB边上,点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)若△ABC的底边长5,周长为21,求△BCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知I是△ABC的内心,AI延长线交△ABC外接圆于D,连BD.
(1)在图1中,求证:DB=DI;
(2)如图2,若AB为直径,且OI⊥AD于I点,DE切圆于D点,求sin∠ADE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com