
 如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=$\frac{3}{4}$∠AEC.
如图,已知AB∥CD,∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,求证:∠AFC=$\frac{3}{4}$∠AEC. 分析 直接分别过点E,F作ME∥AB,NF∥AD,利用平行线的性质结合已知表示出:∠AFC和∠AEC的度数,进而得出答案.
解答 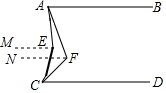 证明:分别过点E,F作ME∥AB,NF∥AD,
证明:分别过点E,F作ME∥AB,NF∥AD,
∵∠EAF=$\frac{1}{4}$∠EAB,∠ECF=$\frac{1}{4}$∠ECD,
∴设∠EAF=x,∠ECF=y,
则∠EAB=4x,∠ECD=4y,
故∠BAF=3x,∠DCF=3y,
∵AB∥CD,ME∥AB,NF∥AD,
∴AB∥ME∥NF∥DC,
∴∠BAF=∠AFN=3x,∠BAE=∠AEM=4x,∠MEC=∠ECD=4y,∠NFC=∠FCD=3y,
∴∠AEC=∠AEM+∠MEC=4(x+y),
∠AFC=∠AFN+∠NFC=3(x+y),
∴∠AFC=$\frac{3}{4}$∠AEC.
点评 此题主要考查了平行线的性质,正确作出辅助线是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
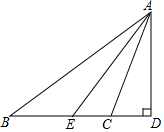 如图所示,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.
如图所示,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把两个含有45°的三角尺如图放置,∠ECD=ACB=90°,且AB=AE,连接AD交BE于点P,试说明:
如图,把两个含有45°的三角尺如图放置,∠ECD=ACB=90°,且AB=AE,连接AD交BE于点P,试说明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com