
如图,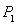 .
.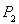 是反比例函数
是反比例函数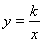 (k>0)在第一象限图象上的两点,点
(k>0)在第一象限图象上的两点,点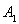 的坐标为(2,0),若△
的坐标为(2,0),若△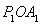 与△
与△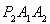 均为等边三角形.
均为等边三角形.
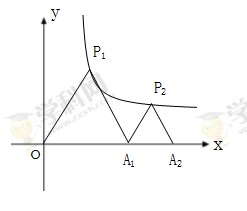
(1)求此反比例函数的解析式;
(2)求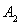 点的坐标.
点的坐标.
(1)反比例函数的解析式是: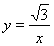 ;(2)A2(
;(2)A2(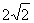 ,0).
,0).
【解析】
试题分析:(1)由于△P1OA1为等边三角形,作P1C⊥OA1,垂足为C,由等边三角形的性质及勾股定理可求出点P1的坐标,根据点P1是反比例函数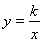 图象上的一点,利用待定系数法求出此反比例函数的解析式;
图象上的一点,利用待定系数法求出此反比例函数的解析式;
(2)作P2D⊥A1A2,垂足为D.设A1D=a,由于△P2A1A2为等边三角形,由等边三角形的性质及勾股定理,可用含a的代数式分别表示点P2的横.纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出A2点的坐标..
试题解析:(1)作P1B⊥OA1于点B ,
∵等边△P1OA1中,OA1=2,
∴OB=1,P1B=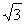 ,
,
把P1点坐标(1,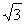 )代入
)代入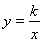 ,
,
解得: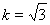 ,
,
∴反比例函数的解析式是: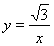 ;
;
(2)作P2C⊥A1A2于点C,
∵等边△P2A1A2,设A1C=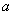 ? 则P2C=
? 则P2C=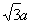 ,OC=2+
,OC=2+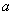 ,
,
把P2点坐标(2+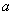 ,
,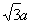 )代入
)代入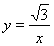 ,
,
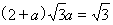 ?? 解得
?? 解得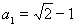 ,
,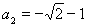 ,
,
OA2=2+2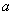 =
=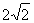 ,
,
∴A2(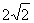 ,0).
,0).
考点:反比例函数综合题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
 如图,是反比例函数y=
如图,是反比例函数y=| m-5 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•德宏州)如图,是反比例函数y=
(2013•德宏州)如图,是反比例函数y=| m-5 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•济宁)如图,是反比例函数y=
(2012•济宁)如图,是反比例函数y=| k-2 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•成都一模)如图,是反比例函数y=
(2013•成都一模)如图,是反比例函数y=| k1 |
| x |
| k2 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,是反比例函数y=
如图,是反比例函数y=| 5-k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com