
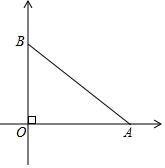
 甲、乙两位探险者今年到沙漠进行探险,没有了水,需要寻找水源,为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为12千米,早晨8:00甲先出发,他以4千米/时的速度向东行走,1小时后乙出发,他以6千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?
甲、乙两位探险者今年到沙漠进行探险,没有了水,需要寻找水源,为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为12千米,早晨8:00甲先出发,他以4千米/时的速度向东行走,1小时后乙出发,他以6千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?  金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )
如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB、CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是( )| A. | 2米 | B. | 2.5米 | C. | 2.4米 | D. | 2.1米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $5\sqrt{3}π$ | B. | $5\sqrt{3}$ | C. | $3\sqrt{3}π$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,D为$\widehat{AC}$的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.
如图,AB为⊙O的直径,D为$\widehat{AC}$的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com