
【题目】为了了解某校学生的身高状况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制如图所示的统计图表.

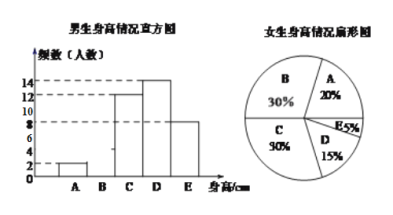
已知女生身高在A组的有8人,根据图表中提供的信息,回答下列问题:
(1)补充图中的男生身高情况直方图,男生身高的中位数落在_______组(填组别字母序号);
(2)在样本中,身高在150≤x<155之间的人数共有_______人,身高人数最多的在____组(填组别序号);
(3)已知该校共有男生400人,女生420人,请估计身高不足160的学生约有多少人?
【答案】(1)补充直方图见解析,D;(2)(2)16,C;(3)估计身高不足160的学生约有516人
【解析】
(1)利用女生身高在A组的人数除以所占百分比计算出女生的总人数即为男生的总人数,用总人数减去A、C、D、E的人数求出B组的人数,即可补全条形图;根据中位数的定义即可得出男生身高的中位数落在D组;
(2)将位于这一小组内的频数相加即可求得结果;
(3)分别用样本中男女生身高不足160的百分比乘以男女生的人数,相加即可得解.
解:(1)女生身高在A组的有8人,所占的百分比为20%,
所以女生的总人数为:8÷20%=40人,
所以男生总人数也为40人,
所以男生身高在B组的有:40-2-12-14-8=4人,
补全条形图如图所示:
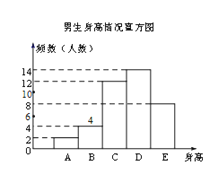
∵男生总人数为40人,
∴中位数是第20和第21人的平均数,
∴男生身高的中位数落在D组;
(2)在样本中,身高在150≤x<155之间的人数共有4+12=16人,身高人数最多的在C组,
故答案为:16、C;
(3)400×![]() +420×(20%+30%+30%)=516.
+420×(20%+30%+30%)=516.
答:估计身高不足160的学生约有516人.


科目:初中数学 来源: 题型:
【题目】已知BC∥OA,∠B=∠A=100°,试回答下列问题:

(1)如图①所示,试说明OB∥AC;
(2)如图②,若点E,F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于________(在横线上填上答案即可);
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB∶∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值;
(4)在(3)的条件下,在平行移动AC的过程中,若使∠OEB=∠OCA,此时∠OCA的度数等于________(在横线上填上答案即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
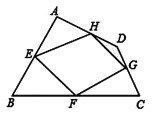
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)四边形EFGH的形状是_____,证明你的结论;
(2)当四边形ABCD的对角线满足_____条件时,四边形EFGH是矩形(不证明)
(3)你学过的哪种特殊四边形的中点四边形是矩形?_____(不证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点的初始位置位于数轴上表示1的点,现对A点做如下移动:第1次向左移动3个单位长度至B点,第2次从B点向右移动6个单位长度至C点,第3次从C点向左移动9个单位长度至D点,第4次从D点向右移动12个单位长度至E点,…,依此类推.这样第_____次移动到的点到原点的距离为2018.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G.若BG=4 ![]() ,则△CEF的面积是( )
,则△CEF的面积是( ) 
A.![]()
B.2 ![]()
C.3 ![]()
D.4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,CQ的长为( )
A.5
B.7
C.8
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
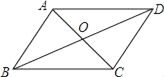
A. OA=OC,AD∥BC B. ∠ABC=∠ADC,AD∥BC
C. AB=DC,AD=BC D. ∠ABD=∠ADB,∠BAO=∠DCO
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com