解:(1)在Rt△AOB中,∵OA=3,sin∠OAB=

,
∴cos∠OAB=

,
∴AB=5,OB=4,BP=5-3=2,
在Rt△APM中,
=cos∠OAB=

,
∴AM=5,OM=2,
点M(0,-2),
又△NPB∽△AOB
∴

=
,BN=

∴ON=OB-BN=4-

=

∴点N(

,0)
设MP的解析式为y=kx+b,
∵MP经过M、N两点,
∴得

,
解得

,
∴MP的解析式为y=

x-2.
设过M、N、B的抛物线解析式为y=a(x-

)(x-4),
且点M(0,-2),可得a=-

,
∴抛物线的解析式为y=-

(x-

)(x-4),
即y=-

x
2+

x-2.
(2)①四边形OMCB是矩形.
证明:在⊙A不动、⊙B运动变化过程中,
恒有∠BAO=∠MAP,OA=AP,∠AOB=∠APM=90°,
∴△AOB≌△APM,
∴OB=PM,AB=AM,
∴PB=OM,而PB=PC,
∴OM=BC
由切线长定理知MC=MP,
∴MC=OB,
∴四边形MOBC是平行四边形.
又∵∠MOB=90°,
∴四边形MOBC是矩形.
②存在.由上证明可知Rt△MON≌Rt△BPN,
∴BN=MN
因此在过M、N、B三点的抛物线内有以BN为腰的等腰三角形MNB存在
由抛物线的轴对称性可知,在抛物线上必有一点Mn与M关于其对称轴对称,
∴BN=BMn
这样得到满足条件的三角形有两个,△MNB和△MnNB.
分析:(1)已知了A的坐标可得出圆A的半径,在直角三角形OAB中,可根据OA的长和∠OAB的正弦值求出AB和OB的长,进而可得出圆B的半径长.也就求出了B点、M点的坐标.
根据相似三角形BPN和BOA可求出BN的长,进而可求出ON的长,也就得出了N点的坐标,可根据M、N、B三点的坐标,用待定系数法求出抛物线的解析式.
(2)①应该是矩形,不难得出△OAB和△PAM全等,那么OB=MP,AM=AB(也可通过圆A的半径长和∠OAB的正切值来求出),由于MP、MC都是圆B的切线,根据切线长定理可得出MP=MC=OB,而OM=BC=AM-OA=AB-AP,由此可得出四边形OBCM是平行四边形.由于∠BOM是直角,因此四边形OBCM是矩形.
②存在,根据①不难得出BN=MN,而M点也在抛物线上,根据抛物线的对称性可知,点M关于抛物线对称轴对称的点Mn也一定符合这样的条件.因此满足条件的三角形有两个,△MNB和△MnNB.
点评:本题着重考查了待定系数法求二次函数解析式、三角形全等、矩形的判定、等腰三角形的判定等知识点,综合性强,考查学生数形结合的数学思想方法.

 ⊙A外切于点P,两圆的公切线MP交y轴于点M,交x轴于点N.
⊙A外切于点P,两圆的公切线MP交y轴于点M,交x轴于点N. ,求直线MP的解析式及经过M、N、B三点的抛物线的解析式.
,求直线MP的解析式及经过M、N、B三点的抛物线的解析式. ,
, ,
,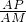 =cos∠OAB=
=cos∠OAB= ,
, =
=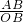 ,BN=
,BN=
 =
=
 ,0)
,0) ,
, ,
, x-2.
x-2. )(x-4),
)(x-4), ,
, (x-
(x- )(x-4),
)(x-4), x2+
x2+ x-2.
x-2.

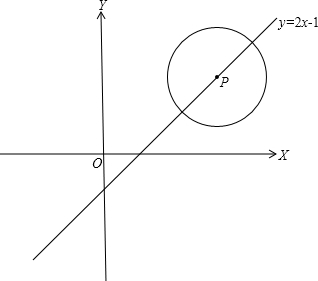 如图,已知⊙P圆心P在直线y=2x-1的图象上运动.
如图,已知⊙P圆心P在直线y=2x-1的图象上运动.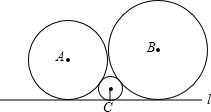
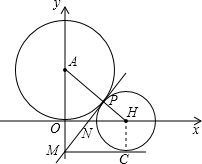
 如图,已知圆心A(0,3),⊙A与x轴相切,⊙B的圆心在x轴的正半轴上,且⊙B与⊙A外切于点P,两圆的公切线MP交y轴于点M,交x轴于点N.
如图,已知圆心A(0,3),⊙A与x轴相切,⊙B的圆心在x轴的正半轴上,且⊙B与⊙A外切于点P,两圆的公切线MP交y轴于点M,交x轴于点N. (2013•太仓市二模)如图,已知圆心为C(0,1)的圆与y轴交于A,B两点,与x轴交于D,E两点,且DE=4
(2013•太仓市二模)如图,已知圆心为C(0,1)的圆与y轴交于A,B两点,与x轴交于D,E两点,且DE=4