【题目】已知二次函数
的部分图象如图所示，则关于
的一元二次方程
的解为 ．
【答案】x1=-1或x2=3．
【解析】
试题分析：由二次函数y=-x2+2x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标，然后可以求出另一个交点坐标，再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程-x2+2x+m=0的解．
试题解析：依题意得二次函数y=-x2+2x+m的对称轴为x=1，与x轴的一个交点为（3，0），
∴抛物线与x轴的另一个交点横坐标为1-（3-1）=-1，
∴交点坐标为（-1，0）
∴当x=-1或x=3时，函数值y=0，
即-x2+2x+m=0，
∴关于x的一元二次方程-x2+2x+m=0的解为x1=-1或x2=3．
每日10分钟口算心算速算天天练系列答案科目：初中数学 来源： 题型：
【题目】我们规定，若关于 x 的一元一次方程 ax=b 的解为 x=ba，则称该方程的为差解方程，例如：3x=
的解为x=
且=-3，则该方程3x=就是差解方程.
请根据以上规定解答下列问题
(1)若关于 x 的一元一次方程-5x=m+1 是差解方程，则 m=_____.
(2)若关于 x 的一元一次方程 2x=ab+3a+1 是差解方程，且它的解为 x=a，求代数式（ab+2）2019的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
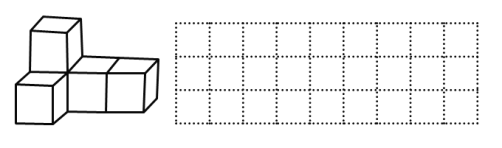
【题目】下图是由大小相同的小立方体搭乘的几何体：
（1）请在所给的方格中画出该几何体从上面看和从左面看的两个图形；
（2）现在你的手里还有一些相同的小立方块，如果保持从上面来看和从左面看所得到的图形不变，则在左边的立体图形中最多可以添加 个小立方块.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）已知∠ABC=90°，∠CBD=30°，BP平分∠ABD，请补全图形，并求∠ABP的度数.
（2）在（1）的条件下，若∠ABC=α，∠CBD=β，直接写出∠ABP的度数.
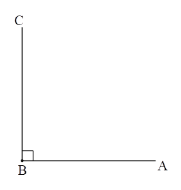
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图7所示，点
、
、
在
轴上，且
，分别过点、、作
轴的平行线，与反比例函数
的图象分别交于点
、
、
，分别过点
作轴的平行线，分别与轴交于点
，连接
，那么图中阴影部分的面积之和为___________.
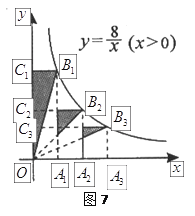
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料，并回答问题：
材料：数学课上，老师给出了如下问题．
如图1，点A、B、C均在直线l上，AB = 8，BC = 2，M是AC的中点，求AM的长．
小明的解答过程如下：
解：如图2，
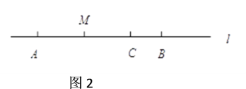
∵ AB = 8，BC = 2，
∴ AC = AB－BC = 8－2 = 6．
∵ M是AC的中点，
∴ 
（ ① ）．
小芳说：“小明的解答不完整”．
问题：（1）小明解答过程中的“①”为 ；
（2） 你同意小芳的说法吗？如果同意，请将小明的解答过程补充完整；如果不同意，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y=﹣x2+bx+c交x轴于点A（﹣3，0）和点B，交y轴于点C（0，3）．
（1）求抛物线的函数表达式；
（2）若点P在抛物线上，且S△AOP=4SBOC，求点P的坐标；
（3）如图b，设点Q是线段AC上的一动点，作DQ⊥x轴，交抛物线于点D，求线段DQ长度的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点A(
，1)在射线OM上，点B(，3)在射线ON上，以AB为直角边作Rt△ABA1，以BA1为直角边作第二个Rt△BA1B1，以A1B1为直角边作第三个Rt△A1B1A2，
，依此规律，得到Rt△B2017A2018B2018，则点B2018的纵坐标为__．
查看答案和解析>>
科目：初中数学 来源： 题型：
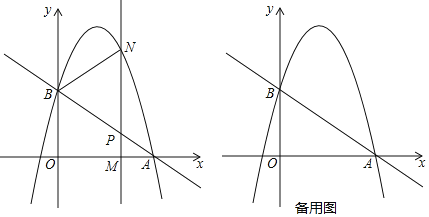
【题目】如图，抛物线
过点
， 
． 
为线段OA上一个动点（点M与点A不重合），过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N．
（1）求直线AB的解析式和抛物线的解析式；
（2）如果点P是MN的中点，那么求此时点N的坐标；
（3）如果以B，P，N为顶点的三角形与
相似，求点M的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com