
 ��ͼ��ʾ����ֱ֪��y=kx+m��x�ᡢy��ֱ���A��C���㣬������y=-x2+bx+c����A��C���㣬��B����������x�����һ�����㣬��x=-$\frac{1}{2}$ʱ��yȡ���ֵ$\frac{25}{4}$��
��ͼ��ʾ����ֱ֪��y=kx+m��x�ᡢy��ֱ���A��C���㣬������y=-x2+bx+c����A��C���㣬��B����������x�����һ�����㣬��x=-$\frac{1}{2}$ʱ��yȡ���ֵ$\frac{25}{4}$������ ��1���ȸ���ֱ�ߵĽ���ʽ���A��C�����꣬Ȼ��A��C����������������м�����������ߵĽ���ʽ�������ɸ��������ߵĽ���ʽ���B������꣮
��2�����ݵȸ������ε�����ȵ��ڵױ߱ȣ�����������ε������ʵ����AP��PC=1��3����3AP=PC���������AC�ij���Ȼ���������ۣ�
�ٵ�P���߶�AC��ʱ��AP+PC=AC��3AP=PC���ݴ˿����AP�ij���Ȼ����ݡ�CAB�����Ǻ���ֵ��ͨ���������������ο����P������꣮
�ڵ�P��CA���ӳ�����ʱ��CP-AP=AC��3AP=PC���ݴ˿����AP�ij�������ͬ�٣�
��3������ֱ��y=$\frac{1}{2}$x+a��������y=-x2-x+6�Ľ���ΪM��xM��yM����N��xN��yN����M��N��ࣩ����Rt��MM��O��Rt��ON��N���Ƴ� $\frac{MM��}{ON��}$=$\frac{OM��}{NN��}$����MM��•NN��=ON��•OM�䣬�Ƴ�-xM•xN=yM•yN���ɷ�������ȥy�������ã�x2+$\frac{3}{2}$x+a-6=0�������ø���ϵ����ϵ���г����̼��ɽ�����⣮
�����âٵĽ�������жϣ�
��� �⣺��1����x=0ʱ��y=6��
��C��0��6����
��y=0ʱ��x=-3��
��A��-3��0����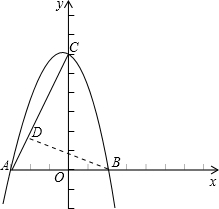
��������y=-x2+bx+c������A��C��
��$\left\{\begin{array}{l}{-9-3b+\\;c=0}\\{c=6}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=-1}\\{c=6}\end{array}\right.$��
�������ߵĽ���ʽΪy=-x2-x+6��
��y=0ʱ��������x2+x-6=0��
��ã�x1=2��x2=-3��
���B��2��0����
��2������B��BD��AC��DΪ���㣬
��S��ABP��S��BPC=1��3��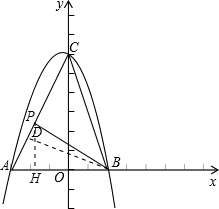
��$\frac{\frac{1}{2}•AP•BD}{\frac{1}{2}•PC•BD}$=$\frac{1}{3}$��
��AP��PC=1��3
�ɹ��ɶ�������AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=3 $\sqrt{5}$��
����PΪ�߶�AC��һ��ʱ������P��PH��x�ᣬ��HΪ���㣬
��PH��OC��
��$\frac{PH}{OC}$=$\frac{AP}{PC}$=$\frac{1}{4}$��
��PH=$\frac{3}{2}$��
��$\frac{3}{2}$=2x+6��
��x=-$\frac{9}{4}$��
���P��-$\frac{9}{4}$��$\frac{3}{2}$��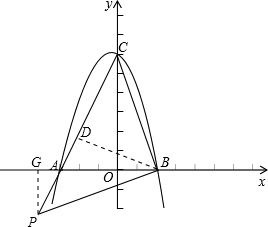
����P��CA�ӳ���ʱ����PG��x�ᣬ��GΪ����
��AP��PC=1��3
��AP��AC=1��2��
��$\frac{PG}{OC}$=$\frac{AP}{AC}$=$\frac{1}{2}$��
��PG=3��
��-3=2x+6
x=-$\frac{9}{2}$��
���P��-$\frac{9}{2}$��-3����
��3���ٴ���a��ֵ��ʹ�á�MON=90�㣬
��ֱ��y=$\frac{1}{2}$x+a��������y=-x2-x+6�Ľ���ΪM��xM��yM����N��xN��yN����M��N��ࣩ
�� $\left\{\begin{array}{l}{{x}_{1}={x}_{M}}\\{{y}_{1}={y}_{M}}\end{array}\right.$Ϊ������ $\left\{\begin{array}{l}{y=\frac{1}{2}x+a}\\{y=-{x}^{2}-x+6}\end{array}\right.$�Ľ�
�ֱ����M��N��MM����x�ᣬNN���x�ᣬ��M��NΪ���㣮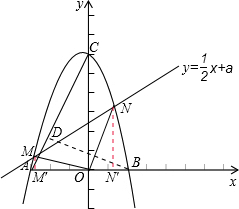 ��M�䣨xM��0����N�䣨xN��0����
��M�䣨xM��0����N�䣨xN��0����
��OM��=-xMON��=xN
�ߡ�MON=90�㣬
���MOM��+��NON��=90�㣬
�ߡ�M��MO+��MOM��=90�㣬
���M��MO=��NON��
��Rt��MM��O��Rt��ON��N��
��$\frac{MM��}{ON��}$=$\frac{OM��}{NN��}$��
��MM��•NN��=ON��•OM�䣬
��-xM•xN=yM•yN��
�ɷ�������ȥy�������ã�x2+$\frac{3}{2}$x+a-6=0��
��xM��xN�Ƿ���x2+$\frac{3}{2}$x+a-6=0����������
�ɸ���ϵ����ϵ�ã�xM+xN=-$\frac{3}{2}$��xM•xN=a-6
�֡�yM•yN=�� $\frac{1}{2}$xM+a���� $\frac{1}{2}$xN+a��=$\frac{1}{4}$xM•xN+$\frac{a}{2}$��xM+xN��+a2=$\frac{1}{4}$��a-6��-$\frac{3}{4}$a+a2
��-��a-6��=$\frac{1}{4}$��a-6��-$\frac{3}{4}$a+a2��
��������2a2+a-15=0
���a1=-3��a2=$\frac{5}{2}$��
�����aֵ��ʹ�á�MON=90�㣬��ֵΪa=-3��a=$\frac{5}{2}$��
���ɢٿ�֪������MON��90��ʱ��a��ȡֵ��ΧΪ-3��a��$\frac{5}{2}$��
���� ���⿼�����ϵ��������κ�������ʽ��ͼ������ļ��㷽�������������ơ�����ͼ�㡢һԪ���η��̸���ϵ����ϵ����Ҫ֪ʶ�㣬�ۺ���ǿ������Ҫ��ϸߣ�����ѧ���������ۣ����ν�ϵ���ѧ˼�뷽����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 13x-1 | B�� | 6x2+13x-1 | C�� | 5x+1 | D�� | -5x-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �������� | B�� | ������ | C�� | �������� | D�� | ���˱��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | sinA=$\frac{12}{5}$ | B�� | cosA=$\frac{12}{13}$ | C�� | tanA=$\frac{12}{5}$ | D�� | tanA=$\frac{12}{13}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com