
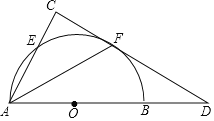
【题目】如图,已知AB是⊙O的直径,⊙O与Rt△ACD的两直角边分别交于点E、F,点F是弧BE的中点,∠C=90°,连接AF.
(1)求证:直线DF是⊙O的切线.
(2)若BD=1,OB=2,求tan∠AFC的值.
【答案】(1)详见解析;(2)![]()
【解析】
(1)连结OF,BE,根得到BE∥CD,根据平行线的性质得到∠OFD=90°,根据切线的判定定理证明;
(2)由OF∥AC可得比例线段求出AC长,再由勾股定理可求得DC长,则能求出CF长,tan∠AFC的值可求.
(1)证明:连结OF,BE,
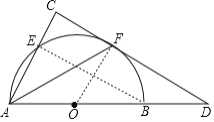
∵AB是⊙O的直径,
∴∠AEB=90°,
∵∠C=90°,
∴∠AEB=∠ACD,
∴BE∥CD,
∵点F是弧BE的中点,
∴OF⊥BE,
∴OF⊥CD,
∵OF为半径,
∴直线DF是⊙O的切线;
(2)解:∵∠C=∠OFD=90°,
∴AC∥OF,
∴△OFD∽△ACD,
∴![]() ,
,
∵BD=1,OB=2,
∴OD=3,AD=5,
∴![]() ,
,
∴CD=![]() =
=![]() =
=![]() ,
,
∵![]() ,
,
∴![]() =
=![]() ,
,
∴tan∠AFC=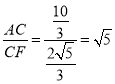 .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
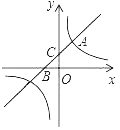
【题目】如图,直线y=x+b与双曲线y=![]() (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的面积为8![]() ,对角线AC长为4
,对角线AC长为4![]() ,M为BC的中点,若P为对角线AC上一动点,则PB与PM之和的最小值为( )
,M为BC的中点,若P为对角线AC上一动点,则PB与PM之和的最小值为( )
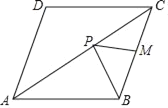
A. ![]() B. 2
B. 2![]() C. 2D. 4
C. 2D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D是平面内一点,连接CD,将线段CD绕C顺时针旋转60°得到线段CE,连接BE,AD,并延长AD交BE于点P.
(1)当点D在图1所在的位置时
①求证:△ADC≌△BEC;
②求∠APB的度数;
③求证:PD+PE=PC;
(2)如图2,当△ABC边长为4,AD=2时,请直接写出线段CE的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD在直线MN的上方BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并直接写出∠FCN的度数(不要写出解答过程)
(3)如图(2),将图中正方形ABCD改为矩形ABCD,AB=6,BC=8,E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变,若∠FCN的大小不变,请求出tan∠FCN的值.若∠FCN的大小发生改变,请举例说明.
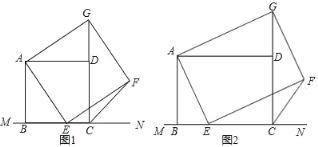
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() 、
、![]() .
.![]() 是线段
是线段![]() 上一动点(点
上一动点(点![]() 不与
不与![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .过点
.过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/18/2206393160556544/2207286529548288/STEM/a9696d0cbdac438aa94c80bfc838afd4.png]
(1)求该抛物线的解析式;
(2)试求线段![]() 的长
的长![]() 关于点
关于点![]() 的横坐标
的横坐标![]() 的函数解析式,并求出
的函数解析式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(x+y)2-2x(x+y); (2)(a+1)(a-1)-(a-1)2;
(3)先化简,再求值:
(x+2y)(x-2y)-(2x3y-4x2y2)÷2xy,其中x=-3,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com