
 如图所示,线段AB=6cm,C点从P点出发以1cm/s的速度沿AB向左运动,D点从B出发以2cm/s的速度沿AB向左运动(C在线段AP上,D在线段BP上)
如图所示,线段AB=6cm,C点从P点出发以1cm/s的速度沿AB向左运动,D点从B出发以2cm/s的速度沿AB向左运动(C在线段AP上,D在线段BP上)分析 (1)根据C、D的运动速度知BD=2PC,再由已知条件PD=2AC求得PB=2AP,所以点P在线段AB上的$\frac{1}{3}$处;
(2)由题设画出图示,根据AQ-BQ=PQ求得AQ=PQ+BQ;然后求得AP=BQ,从而求得PQ与AB的关系;
(3)当C点停止运动时,有CD=$\frac{1}{2}$AB,故AC+BD=$\frac{1}{2}$AB,所以AP-PC+BD=$\frac{1}{2}$AB,再由AP=$\frac{1}{3}$AB,PC=5cm,BD=10cm,再根据M是CD中点,N是PD中点可得出MN的长,进而可得出结论.
解答 解:(1)根据C、D的运动速度知:BD=2PC.
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP,
∴点P在线段AB上的$\frac{1}{3}$处;
(2)如图1:
∵AQ-BQ=PQ,
∴AQ=PQ+BQ;
又∵AQ=AP+PQ,
∴AP=BQ,
∴PQ=$\frac{1}{3}$AB=2cm;
当点Q'在AB的延长线上时,
AQ′-AP=PQ′,
所以AQ′-BQ′=PQ=AB=6cm.
综上所述,PQ=2cm或6cm.
(3)MN的值不变. 理由:如图2,当C点停止运动时,有CD=$\frac{1}{2}$AB=3cm,
理由:如图2,当C点停止运动时,有CD=$\frac{1}{2}$AB=3cm,
∴AC+BD=$\frac{1}{2}$AB=3cm,
∴AP-PC+BD=$\frac{1}{2}$AB=3cm,
∵AP=$\frac{1}{3}$AB=2cm,PC=5cm,
∵M是CD中点,N是PD中点,
∴MN=MD-ND=$\frac{1}{2}$CD-$\frac{1}{2}$PD=$\frac{1}{2}$CP=$\frac{1}{2}$cm.
点评 本题考查了一元一次方程的应用,两点间的距离,灵活运用线段的和、差、倍、分转化线段之间的数量关系是十分关键的一点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016-2017学年江苏省句容市华阳片七年级下学期第一次月考数学试卷(解析版) 题型:单选题
∠1与∠2是两条直线被第三条直线所截的同位角,若∠1=50°,则∠2为( )
A. 50° B. 130° C. 50°或130° D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{{b}^{3}}{2{a}^{3}}$ | B. | -$\frac{{b}^{3}}{6{a}^{3}}$ | C. | -$\frac{{b}^{3}}{8{a}^{3}}$ | D. | $\frac{{b}^{3}}{8{a}^{3}}$ |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片七年级下学期第一次月考数学试卷(解析版) 题型:填空题
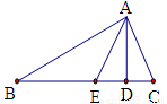
如图,在△ABC中,AD是高,AE是角平分线,∠B=28º,∠C=60º,则∠DAE=______º .
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>0,y2<0 | B. | y1<0,y2<0 | C. | y1•y2<0 | D. | y1+y2<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com