
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
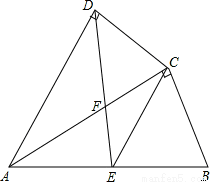
(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求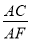 的值.
的值.
(1)证明见解析;(2)证明见解析;(3)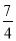 .
.
【解析】
试题分析:(1)由AC平分∠DAB,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=AB•AD;
(2)由E为AB的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE=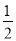 AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得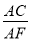 的值.
的值.
试题解析:(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB•AD;
(2)证明:∵E为AB的中点,
∴CE=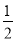 AB=AE,
AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)【解析】
∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=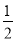 AB,
AB,
∴CE=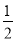 ×6=3,
×6=3,
∵AD=4,
∴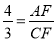 ,
,
∴ .
.
考点:1.相似三角形的判定与性质;2.直角三角形斜边上的中线.


科目:初中数学 来源:2014-2015学年山东省滨州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图所示,给出下列条件:①∠B?∠ACD;②∠ADC?∠ACB;③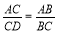 ;④AC2?AD·AB.其中单独能够判定△ABC∽△ACD的个数为( )
;④AC2?AD·AB.其中单独能够判定△ABC∽△ACD的个数为( )
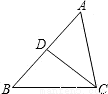
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级11月阶段性检测数学试卷(解析版) 题型:解答题
已知如图1,Rt△ABC和Rt△ADE的直角边AC和AE重叠在一起,AD=AE,∠B=30°,∠DAE=∠ACB=90°.

(1)如图1,填空:∠BAD= ;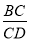 = ;
= ;
(2)如图2,将△ADE绕点A顺时针旋转,使AE到AB边上,∠ACH=∠BCH,连接BH,求∠CBH的度数;
(3)如图3,点P是BE上一点,过A、E两点分别作AN⊥PC、EM⊥PC,垂足分别为N、M,若EM=2,AN=5,求△AND的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级11月阶段性检测数学试卷(解析版) 题型:选择题
则在同一平面直角坐标系中,画出一次函数y=a(x-1)和二次函数y=a(x2-1)的图象只可能是下图中的 ( )
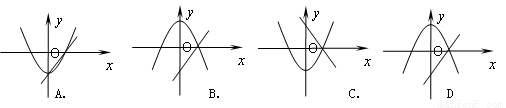
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级11月阶段性检测数学试卷(解析版) 题型:选择题
若关于x的一元二次方程x2-2x-k=0没有实数根,则k的取值范围是( )
A.k>-1 B.k≥-1 C.k<-1 D.k≤-1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市宝应县九年级上学期期末测试数学试卷(解析版) 题型:解答题
已知关于x的方程x2+ax+a-2=0
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市宝应县九年级上学期期末测试数学试卷(解析版) 题型:填空题
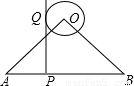
如图,Rt△AOB中,∠O=90°,OA=OB=3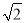 ,⊙O的半径为1,P是AB边上的动点,过点P作⊙O的切线PQ,切点为Q,则切线长PQ的最小值为
,⊙O的半径为1,P是AB边上的动点,过点P作⊙O的切线PQ,切点为Q,则切线长PQ的最小值为
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分10分)已知二次函数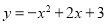 .
.
(1)求函数图像的顶点坐标,并画出这个函数的图像;
(2)根据图像,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当―2<x<2时,函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
二次函数y=x2+bx的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2+bx-m=0(m为实数)在-1<x<4的范围内有解,则m的取值范围是( )
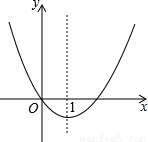
A.m≥-1 B.-1≤m<3 C.3<m<8 D.-1≤m<8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com