
 如图所示的抛物线是把y=-x2经过平移而得到的.这时抛物线过原点O和x轴正向上一点A,顶点为P;
如图所示的抛物线是把y=-x2经过平移而得到的.这时抛物线过原点O和x轴正向上一点A,顶点为P;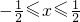 时的最大值和最小值.
时的最大值和最小值. 解:(1)∵抛物线由y=-x2平移得到,
解:(1)∵抛物线由y=-x2平移得到,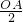 =OM,
=OM,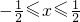 时,当x=
时,当x= 时,y最大=-
时,y最大=- +2×
+2× =
= ;
; 时,y最小=
时,y最小= -2×
-2× =-
=- .
.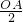 =OM,由此可得出a的值,进而得出其抛物线的解析式;
=OM,由此可得出a的值,进而得出其抛物线的解析式;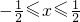 时,当x=
时,当x= 时,y有最大值;当x=-
时,y有最大值;当x=- 时y有最小值.
时y有最小值.

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
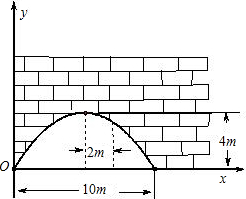 为10m.把它的截面边缘的图形放在如图所示的直角坐标系中.
为10m.把它的截面边缘的图形放在如图所示的直角坐标系中.查看答案和解析>>
科目:初中数学 来源: 题型:
 (1997•陕西)如图所示的抛物线是把y=-x2经过平移而得到的.这时抛物线过原点O和x轴正向上一点A,顶点为P;
(1997•陕西)如图所示的抛物线是把y=-x2经过平移而得到的.这时抛物线过原点O和x轴正向上一点A,顶点为P;| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,排球运动员甲站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行路线是抛物线的一部分.当球运动到最高点D时,其高度为2.6m,离甲站立地点O点的水平距离为6m.球网BC离O点的水平距离为9m,以O为坐标原点建立如图所示的坐标系,乙站立地点M的坐标为(m,0).
如图,排球运动员甲站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行路线是抛物线的一部分.当球运动到最高点D时,其高度为2.6m,离甲站立地点O点的水平距离为6m.球网BC离O点的水平距离为9m,以O为坐标原点建立如图所示的坐标系,乙站立地点M的坐标为(m,0).查看答案和解析>>
科目:初中数学 来源:1997年陕西省中考数学试卷(解析版) 题型:解答题
 时的最大值和最小值.
时的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com