
【题目】如图1,在平画直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,将直线
,将直线![]() 沿
沿![]() 轴向右平移2个单位长度交
轴向右平移2个单位长度交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,交直线
,交直线![]() 于
于![]() .
.

(1)直接写出直线![]() 的解析式为______,
的解析式为______,![]() ______.
______.
(2)在直线![]() 上存在点
上存在点![]() ,使
,使![]() 是
是![]() 的中线,求点
的中线,求点![]() 的坐标;
的坐标;
(3)如图2,在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,22;(2)
,22;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据平移规律“上加下减、左加右减”进行计算可得到平移后的解析式,再分别求出A,B,C的坐标,即可计算出![]() 22;
22;
(2)作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,易得
,易得![]() ,则
,则![]() ,
,
再将x=4代入![]() 得到y=11,所以
得到y=11,所以![]() ;
;
(3)在![]() 轴正半轴上取一点
轴正半轴上取一点![]() ,使
,使![]() ,由外角性质和等腰三角形的性质得出
,由外角性质和等腰三角形的性质得出![]() ,再用勾股定理求得OP的长,即可得出答案.
,再用勾股定理求得OP的长,即可得出答案.
解:(1)直线![]() 沿x轴向右平移2个单位长度,则
沿x轴向右平移2个单位长度,则
y=-2(x-2)-7
=-2x-3
![]()
将![]() 和
和![]() 联立,得
联立,得

解得![]()
![]()
易得![]()
![]()
![]()
故答案为:![]() ,22;
,22;
(2)作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,
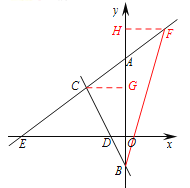
∵![]()
∴![]() ,
,![]() ,
,
∵![]() 为
为![]() 的中线,
的中线,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,
当![]() 时,
时,![]() ,
,
∴![]() .
.
(3)由(1)得![]() ,
,![]() ,
,
∴![]() ,
, ![]() ,
,
在![]() 轴正半轴上取一点
轴正半轴上取一点![]() ,使
,使![]() ,
,
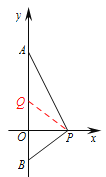
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,由勾股定理可得:
中,由勾股定理可得:![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知BD是矩形ABCD的对角线.

(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
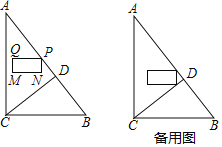
【题目】如图,在△ABC中,∠ACB=90°,AC=8,BC=6.CD⊥AB于点D.点P从点A出发,以每秒1个单位长度的速度沿线段AB向终点B运动.在运动过程中,以点P为顶点作长为2,宽为1的矩形PQMN,其中PQ=2,PN=1,点Q在点P的左侧,MN在PQ的下方,且PQ总保持与AC垂直.设P的运动时间为t(秒)(t>0),矩形PQMN与△ACD的重叠部分图形面积为S(平方单位).
(1)求线段CD的长;
(2)当矩形PQMN与线段CD有公共点时,求t的取值范围;
(3)当点P在线段AD上运动时,求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,tan∠BAC=![]() . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
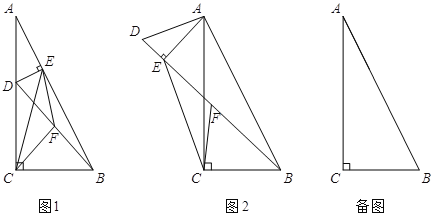
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设![]() ,则k= ;
,则k= ;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )

A.5 B.6 C.2![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.下列结论中正确的有( )
(1)ED=EC;(2)OD=OC;(3)∠ECD=∠EDC;(4)EO平分∠DEC;(5)OE⊥CD;(6)直线OE是线段CD的垂直平分线.
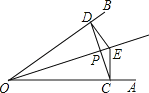
A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,折线BCD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,根据图象解答下列问题:
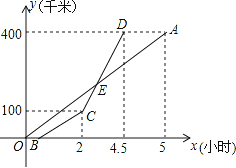
(1)求线段CD对应的函数表达式;
(2)求E点的坐标,并解释E点的实际意义;
(3)若已知轿车比货车晚出发2分钟,且到达乙地后在原地等待货车,则当x= 小时,货车和轿车相距30千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条24cm的细绳围成一个等腰三角形。
(1)如果腰长是底边的2倍,那么各边的长是多少?
(2)能围成有一边长为4cm的等腰三角形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小王星期天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接八位乘客的行车里程(单位:![]() ):-3,+6,-1,-2,+4,-2,+5,-4.
):-3,+6,-1,-2,+4,-2,+5,-4.
问:(1)将最后一位乘客送到目的地时,小王在什么位置?
(2)若汽车耗油量为![]() ,这天上午小王接送乘客,出租车共耗油多少升?
,这天上午小王接送乘客,出租车共耗油多少升?
(3)若出租车的起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.5元,则小王这天上午共得车费多少元?
),超过部分每千米1.5元,则小王这天上午共得车费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com