
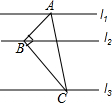
 如图,在△ABC中,∠BAC=60°,∠ABC=90°,直线l1∥l2∥l3,l1与l2之间距离是1,l2与l3之间距离是2,且l1,l2,l3分别经过点A,B,C,则边AC的长为$\frac{2}{3}$$\sqrt{21}$.
如图,在△ABC中,∠BAC=60°,∠ABC=90°,直线l1∥l2∥l3,l1与l2之间距离是1,l2与l3之间距离是2,且l1,l2,l3分别经过点A,B,C,则边AC的长为$\frac{2}{3}$$\sqrt{21}$. 分析 过点B作EF⊥l2,交l1于E,交l3于F,在Rt△ABC中运用三角函数可得$\frac{BC}{AB}$=$\sqrt{3}$,易证△AEB∽△BFC,运用相似三角形的性质可求出FC,然后在Rt△BFC中运用勾股定理可求出BC,再在Rt△ABC中运用三角函数就可求出AC的值.
解答 解:如图,过点B作EF⊥l2,交l1于E,交l3于F,如图.
∵∠BAC=60°,∠ABC=90°,
∴tan∠BAC=$\frac{BC}{AB}$=$\sqrt{3}$.
∵直线l1∥l2∥l3,
∴EF⊥l1,EF⊥l3,
∴∠AEB=∠BFC=90°.
∵∠ABC=90°,
∴∠EAB=90°-∠ABE=∠FBC,
∴△BFC∽△AEB,
∴$\frac{FC}{EB}$=$\frac{BC}{AB}$=$\sqrt{3}$.
∵EB=1,∴FC=$\sqrt{3}$.
在Rt△BFC中,
BC=$\sqrt{B{F}^{2}+F{C}^{2}}$=$\sqrt{{2}^{2}+(\sqrt{3})^{2}}$=$\sqrt{7}$.
在Rt△ABC中,sin∠BAC=$\frac{BC}{AC}$=$\frac{\sqrt{3}}{2}$,
AC=$\frac{2BC}{\sqrt{3}}$=$\frac{2\sqrt{7}}{\sqrt{3}}$=$\frac{2\sqrt{21}}{3}$.
故答案为$\frac{2\sqrt{21}}{3}$.
点评 本题主要考查了相似三角形的判定与性质、三角函数、特殊角的三角函数值、勾股定理、平行线的判定与性质、同角的余角相等等知识,构造K型相似是解决本题的关键.


科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,D、E分别是边AB和AC上的点,将这个△ABC纸片沿DE折叠,点A落到点F的位置.如果DF∥BC,∠B=60°,∠CEF=20°,那么∠A=50度.
如图,在△ABC中,D、E分别是边AB和AC上的点,将这个△ABC纸片沿DE折叠,点A落到点F的位置.如果DF∥BC,∠B=60°,∠CEF=20°,那么∠A=50度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
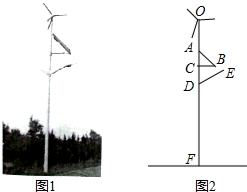
 一数学兴趣小组为了测量河对岸树AB的高,在河岸边选择一点C,从C处测得树梢A的仰角为45°,沿BC方向后退10米到点D,再次测得A的仰角为30°,求树高.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
一数学兴趣小组为了测量河对岸树AB的高,在河岸边选择一点C,从C处测得树梢A的仰角为45°,沿BC方向后退10米到点D,再次测得A的仰角为30°,求树高.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
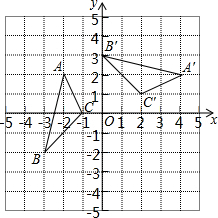 如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )| A. | (0,1) | B. | (1,-1) | C. | (0,-1) | D. | (1,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | [x]=x(x为整数) | B. | 0≤x-[x]<1 | C. | [x+y]≤[x]+[y] | D. | [n+x]=n+[x](n为整数) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
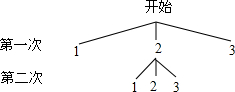 老师和小明同学玩数学游戏.老师取出一个不透明的口袋,口袋中装有三张分别标有数字1,2,3的卡片,卡片除数字外其余都相同,老师要求小明同学两次随机抽取一张卡片,并计算两次抽到卡片上的数字之积是奇数的概率.于是小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果.如图是小明同学所画的正确树状图的一部分.
老师和小明同学玩数学游戏.老师取出一个不透明的口袋,口袋中装有三张分别标有数字1,2,3的卡片,卡片除数字外其余都相同,老师要求小明同学两次随机抽取一张卡片,并计算两次抽到卡片上的数字之积是奇数的概率.于是小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果.如图是小明同学所画的正确树状图的一部分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com